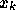 に対する代数方程式をとかないといけ
ない。この解き方について簡単に説明しておこう。
に対する代数方程式をとかないといけ
ない。この解き方について簡単に説明しておこう。
さて、上のようなわけで陰的公式というものが構成できるということはわかっ
たが、これを実際に使うには、 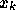 に対する代数方程式をとかないといけ
ない。この解き方について簡単に説明しておこう。
に対する代数方程式をとかないといけ
ない。この解き方について簡単に説明しておこう。
代数方程式といっても、ここで扱うものはほとんど必ず
の形、すなわち、ある関数の不動点を求めるという形になっている。この時は、 以下のような反復を繰り返すことによって解くという方法が考えられる。

これを直接代入法という。
これは容易にプログラム出来て、実際に広く使われる方法である。が、理論的 にはいろいろ怪しい。つまり、
しかし、陰的ルンゲクッタから出てくる方程式の場合、これで結構うまくいく ことが多い。それがなぜかということを示す前に、一般に直接代入の収束の速 さを調べておこう。
方程式(6.27)の解が x であるとき、 直接代入法での古い近似 解と新しい近似解それぞれの真の解との差は

となる。下の方を変形し、fを展開すれば

となる。従って、
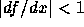 であればよい。
であればよい。
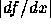 が小さいほど速く収束する。
が小さいほど速く収束する。
話を陰的ルンゲクッタに戻そう。
また、もっとも簡単な中点公式(陰的中点公式)で考えてみる。
解くべき式は、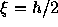 として
として
と書ける。 例によってリプシッツ連続条件
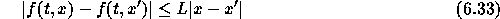
がなり立つとしてよいので、中点公式6.32の右辺の
x による微分が で押えられるということがわかる。つまり、刻み
幅を
で押えられるということがわかる。つまり、刻み
幅を  に比べて小さくとればいいということになる。
に比べて小さくとればいいということになる。
なお、これでは済まないような場合もある。これについては後の「硬い」方程 式のところで扱うことにする。