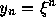 の形をとる。
の形をとる。 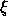 は、安定性多項式と呼ばれる、要
するに
は、安定性多項式と呼ばれる、要
するに 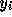 を
を 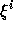 で置き換えてできる代数方程式の根である。このと
き、絶対安定である条件は、すべての
で置き換えてできる代数方程式の根である。このと
き、絶対安定である条件は、すべての  の絶対値が 1 より小さいとい
うことになる。
の絶対値が 1 より小さいとい
うことになる。
一般に線形多段階法についてはオイラー法と同様な扱いができる。つまり、使
う公式を決めたら、それで一変数線形の方程式を解いて見る。すると、それが
一般に 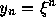 の形をとる。
の形をとる。 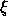 は、安定性多項式と呼ばれる、要
するに
は、安定性多項式と呼ばれる、要
するに 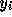 を
を 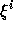 で置き換えてできる代数方程式の根である。このと
き、絶対安定である条件は、すべての
で置き換えてできる代数方程式の根である。このと
き、絶対安定である条件は、すべての  の絶対値が 1 より小さいとい
うことになる。
の絶対値が 1 より小さいとい
うことになる。
例えば、前回の補外法のところで出てきた中点公式

を考えてみよう。安定性多項式は

となり、実解が2つある。すぐにわかるように、 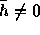 ならば必
ず解の一つは絶対値が 1 より大きいので、中点公式には絶対安定領域がない、
言い替えればかならず不安定であるということがわかる。
ならば必
ず解の一つは絶対値が 1 より大きいので、中点公式には絶対安定領域がない、
言い替えればかならず不安定であるということがわかる。
これにたいし、アダムス法はちゃんと絶対安定領域を持つ。但し、次数が上が るにつれて小さくなるし、陽公式の安定領域は陰公式のそれよりもずっと狭い。