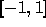 で与えられる直交関数系である。そのk番
目の項
で与えられる直交関数系である。そのk番
目の項 はk次多項式であり以下の性質を持つ。
はk次多項式であり以下の性質を持つ。
前回の資料の最後に書いたように、ガウス型(あるいは、ガウス・ルジャンド
ル型)積分公式は、ルジャンドル多項式の零点を点にとるものである。ルジャ
ンドル多項式は有限区間 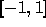 で与えられる直交関数系である。そのk番
目の項
で与えられる直交関数系である。そのk番
目の項 はk次多項式であり以下の性質を持つ。
はk次多項式であり以下の性質を持つ。

定義はいろいろあるが、
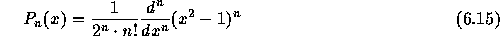
と書かれることが多い。
 の零点とは、
の零点とは、 の解のことである。n次ルジャンドル多項式の場合
実区間
の解のことである。n次ルジャンドル多項式の場合
実区間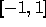 にn個必ず零点がある。これを以下
にn個必ず零点がある。これを以下  と
する。
と
する。
さて、以下でガウス型公式の次数について考える。n点使った時に2n次 になる、いいかえれば 2n-1次までの多項式については厳密な値を与えると いうことが予想されるので、これを示すという方針で考えていく。
任意の 2n-1次多項式 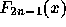 に対して、
に対して、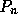 の全ての零点で値が
一致するようなn-1次多項式
の全ての零点で値が
一致するようなn-1次多項式 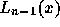 を構成することができる。これを
使うと、
を構成することができる。これを
使うと、

と書ける。ここで、 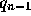 は n-1次の多項式である。これを区間
は n-1次の多項式である。これを区間
 で積分すると、もちろん
で積分すると、もちろん
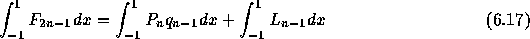
であるが、右辺の第一項の  は n-1次多項式であり、n次ルジャ
ンドル多項式
は n-1次多項式であり、n次ルジャ
ンドル多項式 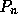 は n-1次以下の任意の多項式と直交するので、この積分
は0になる。つまり、
は n-1次以下の任意の多項式と直交するので、この積分
は0になる。つまり、
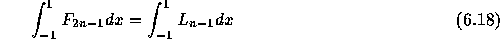
となるわけである。というわけで Fの積分を計算するには Lの積分を求めれ ばいい。ところが、 L は n-1次なので、 n 点での値が決まれば一意に 決まり、積分出来てしまう。
結局、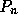 の零点での値を使えば、
の零点での値を使えば、 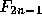 の積分が計算できたことに
なる。
の積分が計算できたことに
なる。
さらに厳密な話としては、 2n-1次よりも高次の項がある関数を近似して積 分したときにどのような誤差項が入ってくるかという議論が必要になるが、こ れは省略する。
一般に、特異点を持たないような性質のよい関数の時には、ガウス型積分公式 は非常に強力な方法であるといえる。
なお、一般の次数の場合、ガウス型公式は

の形をとる。これらの定数の値については適当な参考書を見ること