
ニュートン・コーツ型の公式の一般形についてはすでに説明したが、あれでは 具体的なことが良くわからないと思うので例によって次数が低いものを構成し てみる。

を区間  (これは、すでに適当に分割したあとの狭い区間である
と思って欲しい)で数値的に積分するのに、例えば関数を1度だけ計算すると
すれば、以下のようにいろいろなものが考えられる
(これは、すでに適当に分割したあとの狭い区間である
と思って欲しい)で数値的に積分するのに、例えば関数を1度だけ計算すると
すれば、以下のようにいろいろなものが考えられる

これらは、それぞれ、その区間で関数の値が定数であると近似して、その定数 を積分したというふうに解釈できる。もちろん、中点以外の任意の点をとるこ とも考えられる。
計算精度という観点からは、中点をとることには非常に特別な性質がある。つ
まり、この場合だけ局所誤差が 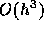 になるのである。これは、テイラー
展開の1次の項が積分すると消えることから容易に示すことができる。という
わけでこれには名前がついていて、中点公式という。
になるのである。これは、テイラー
展開の1次の項が積分すると消えることから容易に示すことができる。という
わけでこれには名前がついていて、中点公式という。
さて、それでは、2度計算していいとすればどうであろうか?普通に考えつく のは先週も書いた台形公式である。つまり、関数を

で近似して、それを積分して求まる

を積分の値として使うわけである。
台形公式の局所誤差は 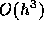 であり、中点公式と同じである。2点も使っ
て、1点しか使わない中点公式と同じでは意味がないと思う人もいるかもしれ
ないが、実はそうでもない。1区間だけを考えるとたしかに台形公式は2点使う
が、ある区間の左端はもちろんその左の区間の右端なので、関数の値は同じだ
からである。つまり、全体をn個の区間に分けた時、中点公式では n回関
数を計算するが、台形公式ではそれより1多い n+1回計算するだけである。
であり、中点公式と同じである。2点も使っ
て、1点しか使わない中点公式と同じでは意味がないと思う人もいるかもしれ
ないが、実はそうでもない。1区間だけを考えるとたしかに台形公式は2点使う
が、ある区間の左端はもちろんその左の区間の右端なので、関数の値は同じだ
からである。つまり、全体をn個の区間に分けた時、中点公式では n回関
数を計算するが、台形公式ではそれより1多い n+1回計算するだけである。
区間の端ではない、一般的な位置に点をとるとすればどうであろうか?以下、
面倒なので区間  で
で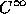 級関数
級関数

の積分をするということにする(適当な変数変換をすればいつでもこう置き換 えられる)。
積分した結果は

となって、テイラー展開の偶数項しか現れないことに注意して欲しい。
2点の x座標を  と
と  としたとき、一般的には数値積分の近
似式が
としたとき、一般的には数値積分の近
似式が
の形になる。これで、上の積分を近似するわけだが、0次の項が消えるために
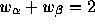 , また奇数次の項が出てこないために
, また奇数次の項が出てこないために
 かつ
かつ である必要があることは
すぐにわかるであろう。
である必要があることは
すぐにわかるであろう。
というわけで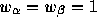 と決まってしまったので、あと
出来ることは
と決まってしまったので、あと
出来ることは  の値を決めることだけである。式
6.11を書き直すと
の値を決めることだけである。式
6.11を書き直すと

となるので、

とすれば、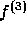 までの項を一致させられるということがわかる。
までの項を一致させられるということがわかる。
台形公式は 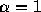 に相当し、
に相当し、 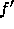 までしか消えていないので、ずいぶ
ん精度が上がっていることがわかるであろう。
そのかわり、区間の端の点の再利用が出来ないので、中点公式に比べて計算量
が2倍になっているということに注意しておく。
までしか消えていないので、ずいぶ
ん精度が上がっていることがわかるであろう。
そのかわり、区間の端の点の再利用が出来ないので、中点公式に比べて計算量
が2倍になっているということに注意しておく。
もうちょっと頑張って3点にしてみよう。等間隔に点をとるなら両端と中点 であり、このときは2次曲線で近似して局所誤差は3次となる。これはいうまで もなくシンプソンの公式である。
不等間隔の時何が実現できるかだが、ここでは具体的に形を書かない。2点の
場合と同様な考察から、区間の中点を1つ、両側に1点づつとると、こんどは
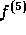 までの項を一致させられるということがわかる。
までの項を一致させられるということがわかる。
ここまでの話だと、