
ハミルトン系のシミュレーションの例には例えば以下のようなものがある
これらはいずれも、古典的な多体問題として定式化される。プラズマの場合は 磁場も入るのでちょっと面倒だが、それを無視すれば運動方程式が

つまり、ある粒子 i の加速度は他のすべての粒子からの力の合計というこ とになる。もちろん、古典力学系は他にもいろいろあるが、基本的なアプロー チは似たようなものである。
このような問題に対して、もっとも普通に使われる公式は以下の leapfrog といわれるものである。
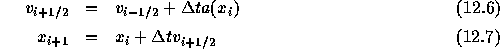
これでは速度と位置がずれた時間でしか定義されない が、出発用公式として

を使い、さらに終了用公式として

を使うことで最初と最後を合わせることが出来る。この形は、実は
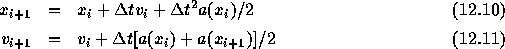
と数学的に等価である(証明してみること)また、以下のようにも書ける

さらにまた、速度を消去して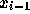 ,
, 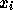 ,
, 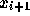 の関係式の形で
かいてあることもあるかもしれない。この時は前回紹介した Stormer-Cowell
公式のもっとも簡単なものと一致する。なお、すべて違う名前がついていたり
するが、結果は丸め誤差を別にすれば完全に同じである。時々、これらが違う
ものであるかのように書いてある教科書があるので注意すること。
の関係式の形で
かいてあることもあるかもしれない。この時は前回紹介した Stormer-Cowell
公式のもっとも簡単なものと一致する。なお、すべて違う名前がついていたり
するが、結果は丸め誤差を別にすれば完全に同じである。時々、これらが違う
ものであるかのように書いてある教科書があるので注意すること。
この公式は局所誤差が  、大域誤差が
、大域誤差が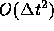 である。
である。
さて、局所誤差という観点からはこれは決して良い公式というわけではないが、 現実にはこの公式は非常に広く使われている。
これは、別にもっとよい方法を知らないからとかではなく、実はこの方法がい くつかの意味で非常に良い方法であるからである。いくつかの意味とは、例え ばエネルギーや角運動量のような保存量が非常によく保存するということであ る。これらの保存量については多くの場合に誤差がある程度以上増えない。
この、ある程度以上誤差が増えないというのは目覚しい性質である。通常の方 法では、エネルギーの誤差は時間に比例して増えていく。従って、長時間計算 をしようとすればそれだけ正確な計算をする必要がある。ところが、エネルギー の誤差は溜っていかないのならば、かならずしも精度を上げる必要はないとも 考えられる。
もちろん、エネルギーが保存していればそれだけで計算が正しいということに はならない。が、理論的には、いくつかの重要な結果が得られている。まず、
Symplectic method については、以下のようなことが知られている
以下、まず数値例でこれらの性質を確認し、それからなぜこのようなうまい性 質を持つのかについて直観的な説明を与えよう(厳密な説明/証明には力学系 の積分可能性に関するかなり深い知識が必要となる)。今週はシンプレクティッ ク公式を扱う。