
能書きを聞いていても良くわからないので、実例を見てみよう。まず、簡単な 例として調和振動子

を leap frog と 2階のルンゲクッタで解いた例を示す。初期条件は  で、時間刻みは
で、時間刻みは  である。
である。
軌道とエネルギーを図に示す。非常に特徴的なのは、 leap frog ではエネル ギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えている ことである。
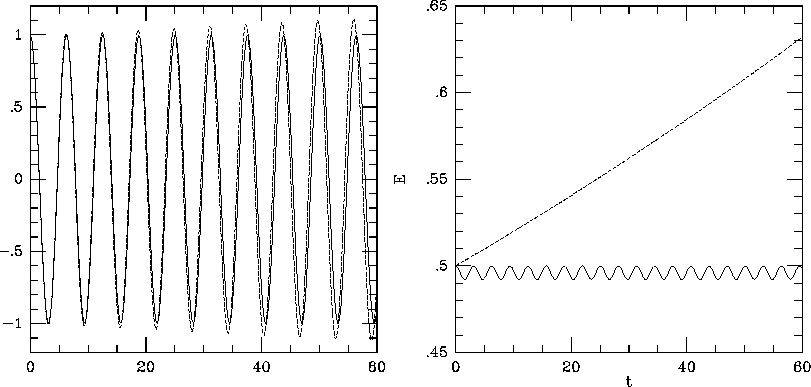
図 12.1: 調和振動子の数値積分。左:軌道。右:エネルギー。破線は2次のル
ンゲクッタ、実線は leapfrog の結果
ルンゲクッタでは単調に変化するというのは前に説明した通り (2階のルンゲクッタでは虚軸を安定領域に含まないため)である。 さて、これに対し、 leapfrog ではエネルギーが変化していないが、これはど ういうことなのであろう?
実は、この調和振動子の場合には、 leapfrog 公式は以下の量

を保存するということを確かめることが出来る。つまり、 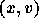 で与えら
れる位相平面の上で考えると、 leapfrog 公式の解は上の式で与えられる楕円
の上にのっているのである。このために、エネルギーの誤差がある値よりも大
きくなり得ないことになる。
で与えら
れる位相平面の上で考えると、 leapfrog 公式の解は上の式で与えられる楕円
の上にのっているのである。このために、エネルギーの誤差がある値よりも大
きくなり得ないことになる。
では、非線形振動ではどうだろう?簡単な例として

を leap frog と 2階のルンゲクッタで解いた例を示す。初期条件は 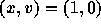 で、時間刻みは
で、時間刻みは 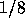 である。
である。
軌道とエネルギーを図に示す。調和振動の場合と同様に、 leap frog ではエネル ギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えている。
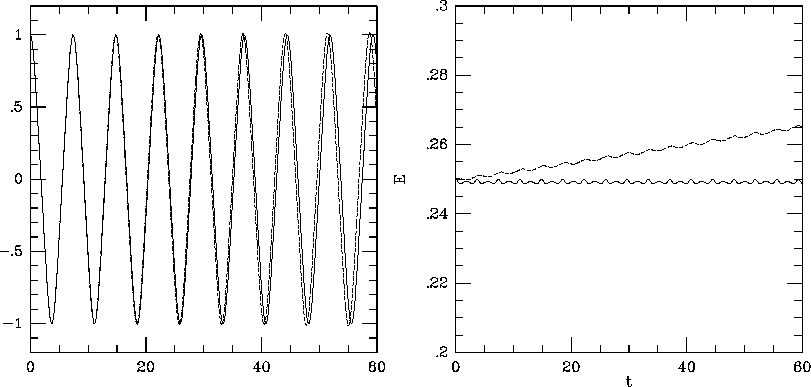
図 12.2: 非線形振動の数値積分。左:軌道。右:エネルギー。破線は2次のル
ンゲクッタ、実線は leapfrog の結果
この場合も保存量があるので、頑張れば求まるかもしれない。