
さて、前の節ではすこし難しい(というか、抽象的な)話をしたが、もうちょっ と具体的にどんな解法があるのかということを考えてみる。比較的古くから研 究され、実用にも使われているのは、2階の微分方程式

に特化した解法である。一般的な方法は、これをそのままいままでに説明して きたいろいろな解法で解くということだが、 v は x の微分に過ぎないの で、例えば線形多段階法の場合にはこれはちょっと無駄な気がする。つまり、 例えばアダムス法で加速度の多項式近似が求まっているとすれば、それを1回 積分すれば速度の変化量がもとまり2回積分すれば位置の変化量がもとまるか らである。この考え方に基づく方法を Stormer-Cowell 法という。この方法の 場合、普通は

という形に書いて、 v を明示的に変数として持たないことが多いが、これ は慣習によるものであまり意味はない。
この方法を普通の方法と比べてみると、計算量(といっても、 f の計算自
体は変わらないが)、メモリ必要量とも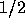 になっていることがわかる。計
算速度等が問題になる場合には、アダムス法ではなくこちらを使うべきである
ということはいうまでもないであろう。
になっていることがわかる。計
算速度等が問題になる場合には、アダムス法ではなくこちらを使うべきである
ということはいうまでもないであろう。
この型の公式は高精度が必要な天体の軌道計算などに広く使われている。ここ では14次とか 16 次の超高次の公式が使われるのが普通である。
さて、例によってもっとも簡単な場合というのを見てみよう。もっとも簡単な
のは右辺が 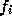 だけの場合、つまり
だけの場合、つまり

というものであり、これを特に Verlet method ということがある。
この方法は Stormer-Cowell 法のなかでもっとも簡単なものだが、後でみるよ うに非常に特別な性質がありもっとも広く使われている。
ルンゲ・クッタについても同様に 2階の方程式専用の公式がある。ここでも、 計算量が減る他、到達可能次数が一般に1階の方程式用の方法よりも高いというこ とが知られている。この型の公式を普通 Runge-Kutta-Nystroem 法と呼ぶ。
陰的な公式の場合は、ガウス公式や Lobatto 公式に比べてよい振舞いをする ものはいまのところ知られていない。陽的なものは多数しられていて、かなり 良く研究されている。
外挿法についても同様なことを考えられるはずであるが、私の知る限りそのよ うな方法は文献には出てこない。