最初に見たように、例えば化学反応系などでタイムスケールが非常に違うと具 合の悪いことが起きるわけであるが、この具合の悪さというのは具体的にはな にかというのが問題である。
例によって、方程式が線形の場合について考える。非線形の場合は、局所的に 線形化することで硬さを定義することになる。非斉次の線形常微分方程式
の一般解は
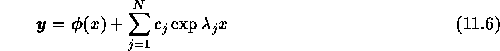
で与えられる。ここで、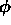
は方程式(11.5) を満たす特殊解
である。
さて、この方程式が安定であるとすれば、固有値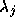 
はすべて実部
が負である。ところで、前回の安定性領域についての議論で見たように、大抵
の数値解法は絶対安定性領域が左側に有界である。これは、言い替えると、時
間刻み h を、適当な定数 M を使って
という制限を満たすようにとらないといけないということを意味する。 M は実際には安定性領域の左側の限界値ということになる。
さて、こういった問題で、どのあたりまで計算しないといけないかというのを 考えると、実部の絶対値が最小の固有値に対応する成分が十分小さくなるまで ということになる。従って、必要なステップ数は、
に比例する程度ということになる。つまり、この値が大きいと、計算が非常に 大変になるのである。この値のことを硬さ stiffness といい、これが「非常 に大きい」ときに方程式が硬いという。
どれくらい大きい時に硬いというかは曖昧であるが、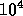 
を越えると硬い
といって間違いない。実用上は、 
を越えることも珍しくない。
なぜ「硬い」といわれるかという歴史的な事情を紹介しておくと、このような 問題は、さいしょ機械制御系、つまり、モーターで棒かなにかを回してその先 の位置をセンサでフィードバックして制御するようなもので発見された。棒を 振り回すとこれは変形するが、棒が「硬い」ほどその変形の周期が短くなる、つま り固有値の絶対値が大きくなるわけである。
なお、この例からわかるように、本当は固有値の虚数部分も問題である。
非線形方程式
の場合には、そのヤコビアン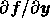
によって局所的
に線形化した方程式について硬さを定義する、つまりはヤコビアンの固有値か
ら決まるということになる。
