さて、硬い微分方程式とは何かということだが、例えば以下のような化学反応 系を考えてみる
各物質の濃度を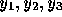 
と書くことにすれば、それぞれの従う方程式は、
例えば
というようなものになる。
係数がたくさんあって面倒なので、以下 
, 
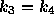とし、初
期条件として
という場合だけを考えることにする。
図11.1
に、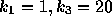 
として、前進オイラー法および後退オイラー法で
解いた場合の数値解の例を示す。この時の定常解は 
というところになる。グラフに示しているのは 
と
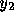である。
滑らかに収束しているのは、前進オイラー法で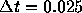 
ととった
ものと後退オイラー法で
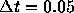ととったものである。これに対し、振動的に発
散してしまっているのは前進で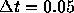 
の場合である。非常に点
が荒く、途中での誤差が大きいが最終的には真の値にいっているのは、後退オ
イラー法で
と極端に刻みを大きくしたものである。
なお、この計算例では、保存則
を利用して、方程式から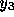 
を消している。
化学反応系のような非線形の方程式系では、上の例のように速度定数が大きく
違うということはそれほど珍しいことではない。上の例では 
であ
るが、これが何桁も大きい場合というのもある。こういった場合にどういう方
法を使うべきかというのが今日考えていきたいことである。
