リチャードソン補外の考えを常微分方程式に適用しようというのがグラッグ法 である。以下のことに注意したい：
これらの問題のために、常微分方程式に対して補外法が使えるということが初 めて示されたのは 1965 年と比較的最近のことである。（線形多段階法やルン ゲ・クッタ法は前世紀から使われている）
陽的な公式で、誤差に奇数次の項がないものを構成できるかというと、これは 実は可能であるということが知られている。もっとも普通に使われるのは、陽 的中点公式と呼ばれる以下の公式である。
これは、前回述べた線形多段階法の一つである。これと、前進オイラー法によ る出発公式
を組み合わせたものは（ステップ数が偶数なら））、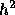 
による漸近展開
をもつことが知られている。従って、この組合せを使うと、リチャードソン補
外によって超高精度の積分公式を作れる。これを通常グラッグ法と呼ぶ。