 以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
線形多段階法の誤差の問題を考えるには、補間多項式の主要誤差が陽的公式と
陰的公式でどう違うかということを考える必要がある。線形多段階法の、特に
大域誤差の理論は難しいので、以下局所誤差について考える。局所誤差を考え
る時に、 以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
一般に、厳密解は独立変数 tによるテイラー展開を持つとしてよいので、 p次の補間多項式で近似したときの主な誤差は p+1次の成分から出てくる。
補間多項式自体の誤差については、以下のような定理が知られている。証明は それほど難しくないので、やってみること。
定理: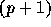 個の標本点
個の標本点  での、関数
での、関数  の値
の値  を標本値とする最小次数補間多項式
を標本値とする最小次数補間多項式 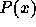 は以下の性質を持つ:
は以下の性質を持つ:
任意の xに対して、 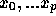 および x を含む最小の閉区間に
および x を含む最小の閉区間に
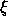 が存在し、
が存在し、
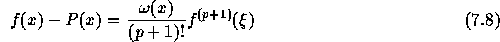
ここで、

である。
ここで、  が問題の区間で一定であると思えば、誤差は
が問題の区間で一定であると思えば、誤差は
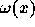 を積分したもので与えられる。
を積分したもので与えられる。
hでの等間隔補間の場合について、  での積分誤差(陰的ア
ダムス公式の誤差)と
での積分誤差(陰的ア
ダムス公式の誤差)と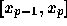 での誤差(陽的アダムス公式の誤差)
の係数を、いくつかの p の場合について下の表にまとめておく(実際の誤差
は
での誤差(陽的アダムス公式の誤差)
の係数を、いくつかの p の場合について下の表にまとめておく(実際の誤差
は 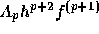 と書ける)。
と書ける)。
すぐにわかるように、陰的公式の誤差は圧倒的に小さい。このために、同じ刻 み幅であれば陰的公式のほうがそれだけ精度がいいことになる。
が、初期推定として陽的公式を使った場合、精度という観点からは、一回だけ
導関数を評価して直接代入したもの (Predict-Evaluate-Correct, PEC) 、あ
るいは反復をもう一回だけするもの [P(EC) ]で十分であり、完全に収束さ
せてもあまり意味がない。これは、精度の向上が、圧倒的とはいえせいぜい
1-2桁であるからである。
]で十分であり、完全に収束さ
せてもあまり意味がない。これは、精度の向上が、圧倒的とはいえせいぜい
1-2桁であるからである。
つまり、反復を繰り返しても、陰的公式の値に近付くが別に真の解には近付か ないのである。