 が、標本点
が、標本点 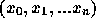 で、関数値
で、関数値
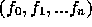 をとるとする。これを、以下のような形の多項式
をとるとする。これを、以下のような形の多項式
さて、補間公式の構成について、まえに説明したのはラグランジュ補間の公式 をそのまま使う方法であった。これはこれで別にいけないわけではないのだが、 もう少しスマートな方法があるので、それを紹介しておく。
補間したい関数  が、標本点
が、標本点 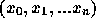 で、関数値
で、関数値
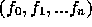 をとるとする。これを、以下のような形の多項式
をとるとする。これを、以下のような形の多項式

という形に書くことを考える。これを、 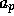 までをとったものは
までをとったものは 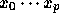 までを通る最低次補間多項式になっているように構成すること
にする。で、低い次数から順に作っていく。付け加える新しい項は、それまで
に使った点すべてで0になるので、新しい点で標本と一致するように
までを通る最低次補間多項式になっているように構成すること
にする。で、低い次数から順に作っていく。付け加える新しい項は、それまで
に使った点すべてで0になるので、新しい点で標本と一致するように 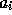 の
値を決めればいい。
の
値を決めればいい。
まず、n=0 については、 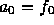 とすればいいのは明らかであろう。
次にn=1 であるが、
とすればいいのは明らかであろう。
次にn=1 であるが、

から

となる。同様に、 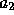 を求めると、
を求めると、

ただし、

である。
さて、段々式が繁雑になるが、もうちょっとの辛抱である。上の形は、

というふうにも書き直せることに注意しよう。これは、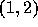 を通る補間式
の一次の係数と、
を通る補間式
の一次の係数と、  を通る補間式の係数の差みたいなものになっている。
を通る補間式の係数の差みたいなものになっている。
ここで、天下りに、 k 階差商 (divided difference)  というものを導入する。これは以下のように定義される。
というものを導入する。これは以下のように定義される。

実は、このように定義された D が、

を満たす、求める係数であることを示すことが出来る。
証明には、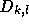 が、
が、  から始まる k+1点を通る補間多項式の係数
であるということを用いる。定義により
から始まる k+1点を通る補間多項式の係数
であるということを用いる。定義により

であるの。 ここで、帰納 法を使って証明することにすると、
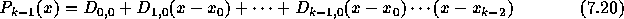
は、  を通る k-1次補間多項式であり、また、
を通る k-1次補間多項式であり、また、
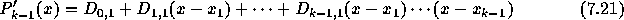
は、  を通る k-1次補間多項式であるとしてよい。こ
の2つの線形結合によって、
を通る k-1次補間多項式であるとしてよい。こ
の2つの線形結合によって、 を通る補間多項式を作るに
は、
を通る補間多項式を作るに
は、

とすればよい。ここで、 と
と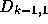 は、それぞれ
は、それぞれ 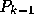 と
と
 の最高次の係数であることに注意すると、
の最高次の係数であることに注意すると、 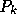 の最高次の係数(これは
の最高次の係数(これは  に等しい)
は、
に等しい)
は、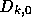 で与えられることがわかる。
で与えられることがわかる。
さて、

という多項式を考えると、これは  で
で  と一致し、
さらに最高次の係数も一致しているので、結局
と一致し、
さらに最高次の係数も一致しているので、結局  であることがわ
かる。つまり、
であることがわ
かる。つまり、 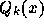 が求める補間多項式であり、
が求める補間多項式であり、 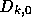 がその最高
次の係数ということになる。
がその最高
次の係数ということになる。