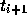 での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に
での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に
さて、前に述べた公式では、補間多項式を陽的に求めた。すなわち、時刻 i
とそれより以前の値だけを使っていた。これに対し、陰的な補間多項式、つま
り 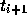 での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に
での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に

の形に書けることになる。また手をぬいて p=1の場合を考えれば、これは単 に台形公式

となる。
陰的公式の場合、例によってどうやって代数方程式を解くかが問題になる。通 常の方法は、
なお、このやり方を、予測子・修正子法と呼ぶ。線形多段階法はほとんどこの 形で使われるため、線形多段階法のことをさして予測子・修正子法と呼ぶ人も いる。