
線形多段階法のなかでもっとも広く使われているのは、アダムス法といわれる クラスの公式である。この原理は、いくつかのステップでの導関数(微分方程 式の右辺) fの値を憶えておいて、それを通る補間多項式を作り、それを積 分して解を求めようというものである。

上の図に概念を示す。ここでは、前回の積分公式と同様にラグランジュ補間 (ニュートン補間)をして多項式を作る。で、その作った多項式を積分する。 例えば、点 i から i+1まで積分するのに、点 i-p から iまでの関数 値を使うとすれば、p次の多項式で
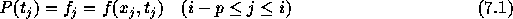
を満たすものを作る。で、i+1での解 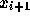 は
は

で与えられる。 刻み hが定数であるとすれば、pを決めれば上の式を

の形に書き直せる。
簡単な例として、 p = 1の場合を考えてみよう。この時、補間多項式は一次 であって

となって、これを積分すれば、結局

となる。
一般に、アダムス法では任意段数の公式が構成でき、その次数は段数に等しい ことがわかっている。これは、ルンゲ・クッタなどに比べればはるかによい性 質をもっているということでもある。