 (仮数)という形になっていて、符号に1ビット(0
なら正、1なら負)、指数に8ビット、仮数に残りの23ビットを使う。
(仮数)という形になっていて、符号に1ビット(0
なら正、1なら負)、指数に8ビット、仮数に残りの23ビットを使う。
さて、前節では、とりあえずもっとも簡単な一変数線形の方程式で極限で厳密 解が得られるということを証明できたわけだが、じつは実際に計算機で計算し てみるとこんなにうまくはいかない。
うまくいかないというのはどういう意味かというと、実際に nをどんどん大 きくしていっても、答が厳密解に近付かなくなるどころかかえって遠ざかって いくということが起きる。これは実際にプログラムをつくって確かめてみれば すぐにわかる。
なぜそういうことが起きるか、また、そうならないようにして意味がある数値 解を得るためにはどうすればいいかというのが、さまざまな数値解法が研究さ れる大きな目標の一つである。ちなみに、もうひとつの目標は、なるべく短い 計算時間で正確な答を得るということである。
計算機で、例えば C でプログラムを書くと、 int と宣言する、普通整 数とよぶデータ型と、 float または double と宣言する、普通「実数」とよぶデータ型 を必要に応じて使い分ける。微分方程式の解を求めようという場合なら、普通 従属変数には double を使うであろう。
計算機を使う時に「実数」と呼ぶものは、数学的な意味での実数とはもちろん 違うものである。なにが違うかというと、基本的には「有限の桁数」しかない ということである。
つまり、数学的な実数というのは、もちろん、連続であるわけで、ということ は、たとえば 1.000.....0001 と 0が何個続いても、そういう実数と いうものはあるわけである。
ところが、計算機では、ある数を有限の情報量(ビット数)で表現する必要が
ある。今のふつうの計算機では、例えば C の float なら 32 ビット、
double なら 64 ビットを使う。例えば float の場合、実際の表現は(符号)
 (仮数)という形になっていて、符号に1ビット(0
なら正、1なら負)、指数に8ビット、仮数に残りの23ビットを使う。
(仮数)という形になっていて、符号に1ビット(0
なら正、1なら負)、指数に8ビット、仮数に残りの23ビットを使う。
仮数は 1 と 2の間を表現すればいいので、 0 を 1 ということにして、オー
ル1 (16進数で 7fffff)を  に割り当てる。指数について
は、正負両方にとるために、 7f のときに
に割り当てる。指数について
は、正負両方にとるために、 7f のときに 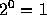 ということにする。
ということにする。
なお、あと、0 というものを表現する必要があるが、これは「全ビット 0 」 が0ということにする。
ちょっと話が細かくなったが、問題は要するに有限の桁数(ビット数)で表現 されているということである。このために、四則演算、あるいは関数計算をし たときに得られる答というものが、厳密に正しいわけではなくなっている。 つまり、無限小数になるものをどこかで打ち切るので、その分誤差がでるわけ である。
なお、打ち切り方には、切捨て、切り上げ、四捨五入などいろいろあり得るが、 最近の計算機は大抵四捨五入になっている。といっても2進数なので0捨1入(最 近接丸め)ということになる。さらに細かいことをいうと、捨てるところがちょ うど 1 の時にどうするべきかという問題があるが、これはさらにその上が 0 になるほうにもっていく(最近接偶数丸め)ということをする計算機もある。
double であれば仮数が52ビット、指数が11ビットになる。