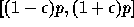4.4 丸め誤差のある場合の収束性

実は丸め誤差がある場合の計算精度の議論というのはかなり難しい。しかし、 このあたりがちゃんとわかってないと、計算して出てきた答が正しいかどうか ということが理解できないので、少し詳しい解説を試みる。

前にやった、線形方程式の例をそのまま使うことにしよう。式ではわからない ので、操作手順（プログラム！）に表してみる。

x = 1;
dt = 1.0/n;
for(i=0;i<n;i++){
   x = x + x*k*dt
}

これにはいくつかの方針がありえる。一つは、「悲観的」解析である。 （区間解析という専門用語がある）つまり、演算毎に、誤差があったら答が最 大これだけずれるというのを見積もって、答の両側に幅をつけていく。 もう一つは、「楽観的」解析（確率的解析ともいう）である。丸めが最近接丸 めであるときには、「計算結果は真の値の回りのある幅で一様分布する」と仮 定してよい場合が多い。この時には、計算結果は確率的に真の値の回りをラン ダム・ウォークすることになる。

これらの2つの方法は原理的には美しいが、実際にはどちらも役に立たないこ とが多い。というのは、現実にはどちらも恐ろしく手間がかかるうえに、悲観 的解析はあまりに悲観的であり、楽観的解析は逆に過度に楽観的であるからで ある。上の例で、どうなるか考えてみる。

このためには、まず、丸め誤差のモデル化が必要である。いま、簡単のために、 任意の演算に対して丸め誤差が以下のように表現できるとする：演算の「真の」 結果が p であるとき、計算機で表現された結果は区間 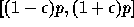の間に一様分布する。

まず、区間解析を試みよう。 面倒なので k=1とし、 k との乗算では 誤差は生じないとする。この時、 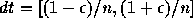となり、 for の最初の反復の後では

で、次の反復ではどうなるかとかいって順に計算していけばいいが、これはあ まりに大変であるので以下の近似を行なう：

• 誤差は x + x*dt の、加算のところだけで出る。

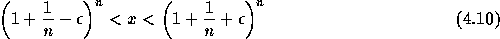
の範囲にくるということになる。

今、 として展開すれば、

ということになり、 n に比例する誤差が入るということになる。

さて、確率的解析の場合にも同様に上の単純化をすると、結果は誤差の平均値 は 0 で分散が 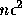の程度ということになる。

実際に計算してみると、区間評価ではで誤差を大きめに、 逆に確率評価ではで小さめに見積もっている。

この、非常に単純な場合には、どちらについてもそのようにずれる理由がわか り、精密な解析を行なえば誤差のもう少し正しい上限を与えることは不可能で はない。が、解くべき方程式や計算法がすこし複雑になると、解析が非常に困 難になることは注意するべきであろう。

なお、一々丸め誤差のことを考えていると話が進まないので、以下、基本的な 話は丸めのことを無視して、必要に応じて丸めの影響を考えることにする。な お、ふつう「打ち切り誤差」という時には、この意味の丸めを無視したものの ことである。