とりあえず、答がわかっている場合にオイラー法がどう振舞うかということを みてみることにしよう。初期値問題
の t=1 での数値解を考える。いうまでもないが、厳密解が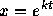 
で
与えられるわけである。
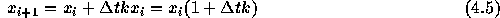
なので、
である。指数関数は定義により
と書けるので、 問題は、この「数値解」がどれくらい正しいかということであるが、
となり、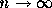
の極限で数値解が厳密解に一致するというこ
とが示せたことになる。上の証明は任意の係数、初期条件と積分区間に一般化
できる。
なお、多変数の場合にもまったく同様に厳密解に収束することが証明できるが、 これは計算練習ということにしておく。各自証明を試みること。