ここまでで見たように、ガウス法などの陰的ルンゲクッタは硬い方程式にたい して非常によい性質をもつが、一つ大きな問題がある。それは、ニュートン法 で解く方程式の大きさが、元の方程式の本数 N と公式の段数 p の積 Np に比例するということである。
ニュートン法で方程式を解くときに、 LU分解（普通のガウスの消去法のこと と思っていい）を使うとすれば、計算量が行列の次元の3乗で増える。つまり、 公式の段数の3乗ということになる。これでは、せっかく高い次数の公式が作 れるといっても実用性は低い。
ニュートン法ででてくる線形化した方程式自体を、LU分解ではなく適当な反復 法、たとえば Gauss-Seidel 法、 SOR、共役勾配(CG)法といったもので解くこ とも考えられるが、これらを使うとまたA-安定性が失われたりすることになる。
これらの問題をあるていど回避するため、非常にさまざまな公式群が研究され ている。以下にその例をあげる
前に述べたように、計算量と精度の関係を見た時に線形多段階法はルンゲクッ タに比べてかなり良いのが普通である。従って、線形多段階法で比較的よい性 質をもつものはないかということを考える。
ダールキストの結果によって、A-安定では2次以上にならないということがわ かってしまっているので、A-安定の条件のほうをちょっと緩めてみる。緩め方 にはいろいろあるが、ギア (C. W. Gear) の提案は、図11.2の ように原点近くで虚部が大きいところでは不安定でもいいということにしよう というものである。
ギアはこのような領域で安定であることを硬安定ということにした。さらに、 以下の形の公式
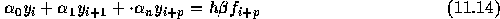
であれば、 
の場合には硬安定な公式が存在することを示した。
係数の表は適当な参考書をみること。
実際のプログラムの例は例えば http://www.netlib.org/ode/cvode.tar.gz といったものを見てみること。
これは無数にある。名前だけをあげると、ローゼンブロック法、 DIRK, MIRK, SIRK, SDIRK といったものがあり、現在盛んに研究されている。
まあ、実用上は、完全陰的なガウスや Radau 公式では問題があるという場合 でなければ、わざわざこれらの方法を使う意味はあまりないように思う。
