Next: 第12章 ハミルトン系とそのための解法
Up: 第11章 硬い微分方程式
Previous: 11.4 完全陰的ルンゲクッタ以外の方法
だいぶいろんなことをやったので、いくつか課題を出しておく。レポートとし
ては、どこまでやるかは各人の自由であるが、採点基準にはどれだけやったか
が入ることはいうまでもないであろう。
- 4次まで(まあ、出来なければ3次とかでもいいけど)の陽的ルンゲクッ
タ公式に対して、安定性を決める多項式(いわゆる安定性因子)を求め、さら
に複素平面上での絶対安定領域を図に示せ。
- 陰的中点公式の安定性について議論せよ。
- 2段4次の陰的ガウス公式について
- ルジャンドル多項式の 0 点をとるということから公式を導け。
- 実際に線形系に適用して、4次精度であることと A-安定であることを確かめよ。
- 2変数以上の場合に適用出来るプログラムを作り、適当な非線形方程式
を解いてみよ。例えば van der Pol 方程式で極度に非線形性の強い場合につ
いて、4次の古典的ルンゲクッタと解の精度、信頼性等を比較してみよ。
- ローレンツのカオス
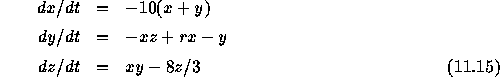
について、
- パラメータ r を変化させた時の定常解の安定性の変化を解析的に調
べよ。
- 適当な数値解法で、数値解を求めてみよ。
- 求まった答が正しいといえるかどうか、またいえるとすればいかなる意
味においてかを議論せよ。
Jun Makino
Thu Aug 13 14:18:16 JST 1998