
線形方程式の場合に、ステップサイズ0の極限で真の解に収束するということ を前に示したわけだが、計算機が実際に計算するときにはもちろん有限のステッ プサイズである。また、上に述べたように丸めの影響があって、どうせ収束は しない。そうすると、どの程度のステップサイズの時に計算精度がどうなるか ということを知る必要がある。
もちろん、プログラムを書いて、真の解との誤差を調べればいいが、もともと 数値解を計算するのは真の解がわからないからなので、そうはいかないわけで ある。
以下、一般の微分方程式に対してオイラー法がどのように収束するかというこ とを考えてみる。先週やった存在定理と同じように、常微分方程式の初期値問題

の 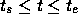 での解を考える。今、 関数f が領域
での解を考える。今、 関数f が領域
 で連続であり、最大値、最小値をもつと
しよう。絶対値が M でおさえられ、
で連続であり、最大値、最小値をもつと
しよう。絶対値が M でおさえられ、 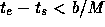 という関係がなりた
つとする。さらに、上の範囲の任意の t, xと
という関係がなりた
つとする。さらに、上の範囲の任意の t, xと  についてリプシッツ条件
についてリプシッツ条件

を満たすものとする。さらに、n, h を、 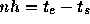 を満たすように
とる(nは整数)。また、 f は 2回以上微分可能であるとする。
を満たすように
とる(nは整数)。また、 f は 2回以上微分可能であるとする。
このとき、オイラー法が一様に一次収束する、すなわち、ある定数Cが存在し、

となることを示すことができる。
こんなのは当たり前と思う人もいるかもしれないが、なかなかそうでもない。
証明の方針としては、例によって具体的に 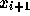 を構成しておく:
を構成しておく:

今、真の解との差が欲しいので、こちらも書いておくと
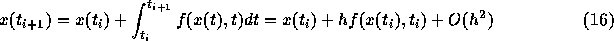
ここで、何故最後の 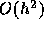 が出てくるかというと、これは f が x,
t のそれぞれで2回以上微分可能としたからである。平均値の定理を適当に
使えばこの形に変形できる。
差をとれば
が出てくるかというと、これは f が x,
t のそれぞれで2回以上微分可能としたからである。平均値の定理を適当に
使えばこの形に変形できる。
差をとれば
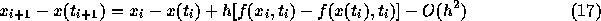
絶対値をとれば

ここで A は定数である。今、

とおいて、さらにリプシッツ条件から変形して

ここで、明らかに  なので、容易に(!)わかるように
なので、容易に(!)わかるように
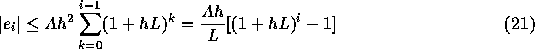
ここで、  であったことを思い出すと
であったことを思い出すと

結局、
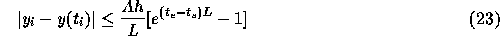
となる。
というわけで、一応、誤差の上限が存在して、それが hに比例するというこ
とが示された。なお、上限の形をみるとなかなか嫌な格好をしていることがわ
かる。つまり、時刻依存性が  の形をしているので、積分を先に進め
ていくと、 かならず誤差が指数関数的に増大していくことになる。これは、
言い換えれば、長時間積分した場合の精度については理論的にはなかなか難し
い問題があるということである。この問題については、より詳しくはまたあと
で扱うことにしよう。
の形をしているので、積分を先に進め
ていくと、 かならず誤差が指数関数的に増大していくことになる。これは、
言い換えれば、長時間積分した場合の精度については理論的にはなかなか難し
い問題があるということである。この問題については、より詳しくはまたあと
で扱うことにしよう。
なお、このような、ある時間範囲で積分したあとの誤差のことを「大域誤差」 という。これに対し、1ステップだけ積分したあとの誤差を局所誤差、あるい は局所離散化誤差という。