2 Euler 法---一変数の場合

まず、一変数の場合を考えよう。微分方程式の初期値問題

に対して、（前進）オイラー法とは以下のような方法である。

時刻 での数値解が 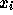であったとすると、時刻 での数値解を

という形に書く。

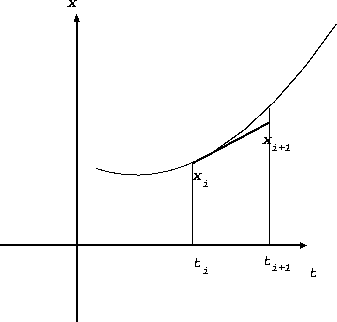
上の図に様子を示す。ここでは、真の解（がわかっているものとして）を曲線 で示し、そこから出発したとした。

やっていることはなんということはなくて、真の解に対する時刻 での 接線を数値解ということにしようということである。

ある時刻 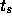での初期条件が与えられて、 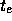での解を求めようという 時に、例えばその区間を n等分して

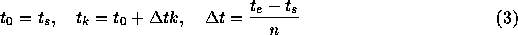
というふうに を決めてやる。あとは 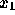から順に 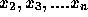と計算していけば、 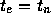での数値解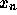 が求まるわけ である。

直観的には、 n を大きくしていけば、正しい答えに近付いていきそうな気 がするであろう。しかし、そうなるということをどうやって証明すればいいで あろうか？

2.1 例：線形方程式の場合

とりあえず、答がわかっている場合にオイラー法がどう振舞うかということを みてみることにしよう。初期値問題

の t=1 での数値解を考える。いうまでもないが、厳密解が で 与えられるわけである。

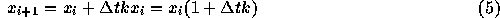
なので、

である。指数関数は定義により

と書けるので、 問題は、この「数値解」がどれくらい正しいかということであるが、

となり、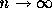の極限で数値解が厳密解に一致するというこ とが示せたことになる。上の証明は任意の係数、初期条件と積分区間に一般化 できる。

なお、多変数の場合にもまったく同様に厳密解に収束することが証明できるが、 これは計算練習ということにしておく。各自証明を試みること。

2.2 計算機の精度

さて、前節では、とりあえずもっとも簡単な一変数線形の方程式で極限で厳密 解が得られるということを証明できたわけだが、じつは実際に計算機で計算し てみるとこんなにうまくはいかない。

うまくいかないというのはどういう意味かというと、実際に nをどんどん大 きくしていっても、答が厳密解に近付かなくなるどころかかえって遠ざかって いくということが起きる。これは実際にプログラムをつくって確かめてみれば すぐにわかる。

なぜそういうことが起きるか、また、そうならないようにして意味がある数値 解を得るためにはどうすればいいかというのが、さまざまな数値解法が研究さ れる大きな目標の一つである。ちなみに、もうひとつの目標は、なるべく短い 計算時間で正確な答を得るということである。

計算機で、例えば C でプログラムを書くと、 int と宣言する、普通整 数とよぶデータ型と、 float または double と宣言する、普通「実数」とよぶデータ型 を必要に応じて使い分ける。微分方程式の解を求めようという場合なら、普通 従属変数には double を使うであろう。

計算機を使う時に「実数」と呼ぶものは、数学的な意味での実数とはもちろん 違うものである。なにが違うかというと、基本的には「有限の桁数」しかない ということである。

つまり、数学的な実数というのは、もちろん、連続であるわけで、ということ は、たとえば 1.000.....0001 と 0が何個続いても、そういう実数と いうものはあるわけである。

ところが、計算機では、ある数を有限の情報量（ビット数）で表現する必要が ある。今のふつうの計算機では、例えば C の float なら 32 ビット、 double なら 64 ビットを使う。例えば float の場合、実際の表現は（符号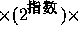） （仮数）という形になっていて、符号に1ビット（0 なら正、1なら負）、指数に8ビット、仮数に残りの23ビットを使う。

仮数は 1 と 2の間を表現すればいいので、 0 を 1 ということにして、オー ル1 （16進数で 7fffff）を に割り当てる。指数について は、正負両方にとるために、 7f のときに 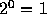ということにする。

なお、あと、0 というものを表現する必要があるが、これは「全ビット 0 」 が0ということにする。

ちょっと話が細かくなったが、問題は要するに有限の桁数（ビット数）で表現 されているということである。このために、四則演算、あるいは関数計算をし たときに得られる答というものが、厳密に正しいわけではなくなっている。 つまり、無限小数になるものをどこかで打ち切るので、その分誤差がでるわけ である。

なお、打ち切り方には、切捨て、切り上げ、四捨五入などいろいろあり得るが、 最近の計算機は大抵四捨五入になっている。といっても2進数なので0捨1入(最 近接丸め)ということになる。さらに細かいことをいうと、捨てるところがちょ うど 1 の時にどうするべきかという問題があるが、これはさらにその上が 0 になるほうにもっていく（最近接偶数丸め）ということをする計算機もある。

double であれば仮数が52ビット、指数が11ビットになる。

2.3 丸め誤差のある場合の収束性

実は丸め誤差がある場合の計算精度の議論というのはかなり難しい。しかし、 このあたりがちゃんとわかってないと、計算して出てきた答が正しいかどうか ということが理解できないので、少し詳しい解説を試みる。

前にやった、線形方程式の例をそのまま使うことにしよう。式ではわからない ので、操作手順を表してみる。

x = 1;
dt = 1.0/n;
for(i=0;i<n;i++){
   x = x + x*k*dt
}

これにはいくつかの方針がありえる。一つは、「悲観的」解析である。 （区間解析という専門用語がある）つまり、演算毎に、誤差があったら答が最 大これだけずれるというのを見積もって、答の両側に幅をつけていく。 もう一つは、「楽観的」解析（確率的解析ともいう）である。丸めが最近接丸 めであるときには、「計算結果は真の値の回りのある幅で一様分布する」と仮 定してよい場合が多い。この時には、計算結果は確率的に真の値の回りをラン ダム・ウォークすることになる。

これらの2つの方法は原理的には美しいが、実際にはどちらも役に立たないこ とが多い。というのは、現実にはどちらも恐ろしく手間がかかるうえに、悲観 的解析はあまりに悲観的であり、楽観的解析は逆に過度に楽観的であるからで ある。上の例で、どうなるか考えてみる。

このためには、まず、丸め誤差のモデル化が必要である。いま、簡単のために、 任意の演算に対して丸め誤差が以下のように表現できるとする：演算の「真の」 結果が p であるとき、計算機で表現された結果は区間 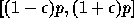の間に一様分布する。

まず、区間解析を試みよう。 面倒なので k=1とし、 k との乗算では 誤差は生じないとする。この時、 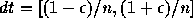となり、 for の最初の反復の後では

で、次の反復ではどうなるかとかいって順に計算していけばいいが、これはあ まりに大変であるので以下の近似を行なう：

• 誤差は x + x*dt の、加算のところだけで出る。

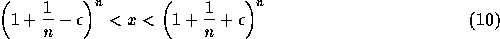
の範囲にくるということになる。

今、 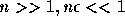として展開すれば、

ということになり、 n に比例する誤差が入るということになる。

さて、確率的解析の場合にも同様に上の単純化をすると、結果は誤差の平均値 は 0 で分散が 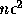の程度ということになる。

実際に計算してみると、区間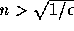評価ではで誤差を大きめに、 逆に確率評価では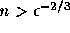で小さめに見積もっている。

この、非常に単純な場合には、どちらについてもそのようにずれる理由がわか り、精密な解析を行なえば誤差のもう少し正しい上限を与えることは不可能で はない。が、解くべき方程式や計算法がすこし複雑になると、解析が非常に困 難になることは注意するべきであろう。

なお、一々丸め誤差のことを考えていると話が進まないので、以下、基本的な 話は丸めのことを無視して、必要に応じて丸めの影響を考えることにする。な お、ふつう「打ち切り誤差」という時には、この意味の丸めを無視したものの ことである。