
4学期の講義のなかで、システム数理 I では線形システムの特に制御理論をあ つかったことと思う。線形システムというのは、基本的に、系が(近似的に) 線形の方程式で記述できる、いいかえれば

の形に書けるもののことである。この系の良いことは、答がわかるということ である。一変数ならもちろんだが、多変数、あるいは高次の導関数があるよう なものでも、線形である限り答えは固有解の重ね合わせでかける。
こういうシステムというのは、工学的な応用上は重要である。例えば、ちょっ と昔のオーディオ機器を考えてみると、これはテープとかレコードに信号が記 録されていて、それを読みとって増幅して音にする。ここで、レコードから信 号を読み出すピックアップ、それを増幅するプリアンプ、メインアンプ、さら にはスピーカのそれぞれが、入ってきた信号をなるべく忠実に増幅したり、あ るいは位置変化を電気信号に変えたり、あるいは電気信号を空気の振動に変え たりする。
そのほか、人工システムというのは、たいてい、線形な振舞いをするようになっ ているものである。これはどうしてかというと、線形でないようなものは設計 のしかたとか、使い方がよくわからないからである。
もちろん、線形の逆の極端になればまたそれは振舞いが簡単になる。その例は ディジタル回路であり、これは線形とは逆に、入力、出力がともに on---off の2値であらわされるわけである。
こういうわけで、例えばエレクトロニクスでは、回路というのは線形(リニア) 回路(アナログというよりリニアの方が使われる)とディジタル回路にわかれ るということになる。
ここで注意しなければいけないことは、こういった、線形とかディジタルとい うのは、あくまでも「理想化」に過ぎないということである。なにがいいたい かといえば、工学的に作ったものでも、理想的に線形であるということはなく かならず非線形性がある。(ディジタルはちょっと話がちがって、理想的であ るといってもいい)
例えば抵抗というものを考える。これはオームの法則

に従うと高校では教わるわけだが、もちろんものごとはそんなに簡単ではない。 簡単ではない理由はいろいろあって、一つはまだ線形の範囲で、インダクタン スとかキャパシタンスがあるということ、もう一つはこれら自体が入力信号に よって変化するということである。どんなふうに変わるかというのはいろいろ あるけれど、例えばどんどん電圧をあげていけば発熱して温度が上がり、抵抗 が大きくなる。もっとどんどん電圧をあげていくといつかは燃えはじめて、切 れてしまったりもするわけである。
バネ、あるいは一般に機械的変形というものを考えても同じことで、ある範囲 では線形に振舞うが変形が大きくなると応答が非線形になり、そのうちに壊れ てしまう。
というわけで、工学的に作るものというのは、わりと線形の範囲で使うものが 多い。これにはいろいろな理由があるが、もっとも大きいものは、 線形 でないと答がわからない ということである。何か目的があってものをつくる わけだから、どう作ったらどう動くかということが簡単に計算出来ないといけ ない。このためには線形性というのは本質的である。
しかし、自然システムの方をみれば、非線形なものはいくらでもある。そういっ たものは、解(つまり、たとえば時間変化)が固有関数では書けない。また、 それだけではなく、多くの場合に「可積分」ではないということがわかってい る。
ここでいう可積分性とは、系の振舞いが十分な数の保存量によって制限されて いて、それらと時間の関数の形に解が書き下せるということである。例えば1 次元調和振動子

を考えてみると、この解というのはxと 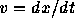 の空間では円上を等角速
度で運動することになる。従って、初期条件がわかれば任意の時刻での「解が
わかる」。数学的には、ハミルトン系(普通の、運動方程式が書けるような系。
ただし、摩擦とかがない理想的なもの)では、自由度の数の2倍マイナス1個だけ
保存量があれば可積分であるということになる。
の空間では円上を等角速
度で運動することになる。従って、初期条件がわかれば任意の時刻での「解が
わかる」。数学的には、ハミルトン系(普通の、運動方程式が書けるような系。
ただし、摩擦とかがない理想的なもの)では、自由度の数の2倍マイナス1個だけ
保存量があれば可積分であるということになる。
N自由度のハミルトン系の状態は 2N次元の空間のなかの1点として表現で き、系の時間発展はそのなかの軌道として表現できる。 大雑把にいうと、保存量が1つ増えれば解(軌道)の存在できる空間が1次元減 る。2N-1あると 1 次元に落ちるわけである。
自由度が増えたり、あるいは非線形の方程式になっても、もちろんこのような 解がある場合というものもある。例えば、太陽の回りの惑星の運動というの は、(惑星が1つだけなら)可積分である。これは、周期解があるということ からも想像がつくであろう。
しかし、惑星が2つになって、そのあいだの相互作用があると、これはもう可 積分ではない。この場合にも、相互作用の効果を近似的に付け加えていく摂動 法のようなものが使える場合もあるが、それでは済まないような場合も無数に ある。
たとえば、図に示すのは、3体問題の計算例である。これは1981年に でた論文からとった図である。こういったものは、周期解に近いと思ってなん とかできるものではないということはわかるであろう。
こういった、面倒な話というのは世の中にいっぱいあって、可積分とか、それ に近いとかいったことを前提にする方法では対応できないわけである。
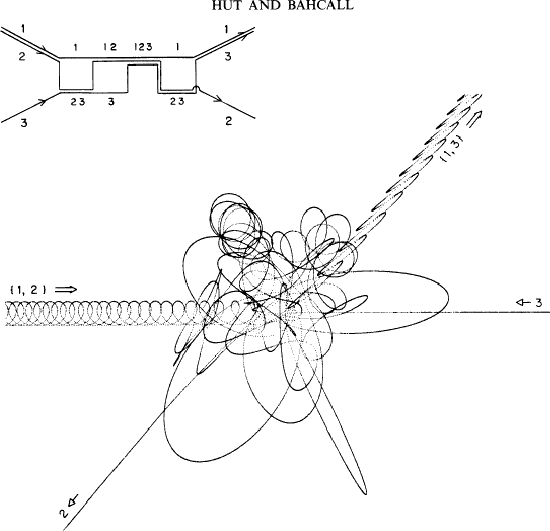
さて、可積分でないといっても、「解がない」わけではない。上の図はまさに そういった解を示しているわけである。
この解を求めるのはどうやったのであろうか?もちろん、計算機で計算しても とめたわけである。しかし、計算してといわれても、実際にどんなプログラム で何を計算したのだろうか?また、この答えは「合っている」のだろうか?そ もそも計算機で求まった答があっているとか間違っているとかはどうやって判 断するのだろうか?
といったようなことを、この講義では考えていくことにしたい。