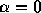 としたものを考えると、これは k<0で
固有値が純虚数になる(
としたものを考えると、これは k<0で
固有値が純虚数になる(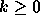 なら非負の実数)固有値が純虚数の時には解
は振幅一定の単振動になり、初期に与えた摂動がそのまま残る。
なら非負の実数)固有値が純虚数の時には解
は振幅一定の単振動になり、初期に与えた摂動がそのまま残る。
さて、上の方程式で 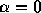 としたものを考えると、これは k<0で
固有値が純虚数になる(
としたものを考えると、これは k<0で
固有値が純虚数になる(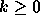 なら非負の実数)固有値が純虚数の時には解
は振幅一定の単振動になり、初期に与えた摂動がそのまま残る。
なら非負の実数)固有値が純虚数の時には解
は振幅一定の単振動になり、初期に与えた摂動がそのまま残る。
このような系は安定平衡点を持たないが、実用上は特別に重要である。という のは、理想化された古典力学系(ハミルトン系)はすべてこのような、安定平 衡点を持たない系であるからである。この場合には安定性の意味が変わる。こ れについては後で扱うことにしたい。