 というものがあって、
というものがあって、
さて、安定性というものを定義しないといけない。そのために、まず、「定常
解の安定性」というものを考えることにする。定常解とは、 要するにある
 というものがあって、
というものがあって、

を満たすもののことである。まあ、 x が微分方程式の右辺に入っていると、 特別な条件の下でなければ定常解はないので、以下

の形、つまり右辺に x が入らないものを考える。これを自律型という。こ の時はもちろん定常解の満たす方程式は

ということになる。
さて、この解が局所的に安定かどうかというのは、以下のような意味であると 考えられるであろう。
「なんらかの理由(外乱とか)で、定常解から少し離れたところに解がいった 時に、もとの解にもどる」ということをさして安定であるという。
ちょっと図に例を示してみよう。左の図のように、盛り上がったところの一番 上にボールかなにかをおいたら、ぴったり頂上におけばそれは止まっている。 つまり、頂上は定常解である。 しかし、すこしでも頂上、すなわち定常解からずれたらそのままころげおちて しまう。これは不安定な定常解ということになろう。

これにたいし、右の図のように谷底ならば、すこしずれたらもとのところの戻 ろうとする。さらに、摩擦や空気抵抗があるから、そのうちにもとのところに止 まる。これは安定解ということになる。
仮に、厳密に水平な面が広がっていたとすれば、少し動かすと動かしたところ でそのまま止まっていることになるであろう。これは中立安定状態ということ になる。
上の説明は直観的ではあるが、ちょっと怪しいところがある。この場合どんな 方程式を考えているのであろうか?例えば以下のような方程式ということになろう:

ここで、 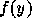 は地面からの力であり、 第二項は抵抗による力である。
抵抗は速度に比例するということにしておく。これはyと
は地面からの力であり、 第二項は抵抗による力である。
抵抗は速度に比例するということにしておく。これはyと 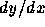 の2変数
の方程式である。
の2変数
の方程式である。
さて、これの定常解(この場合平衡解という言葉をつかうことのほうが多い) の回りで、解がどう振舞うかを調べてみることにする。平衡解は

である。今、

とおいて元の微分方程式を書き直す。この時、 fが

と近似出来ることに注意すると、
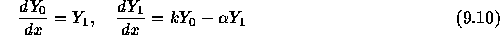
あるいは、行列形式なら

ということになる。これはもちろん以下の形の解を持つ
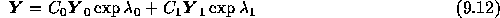
ここで、  と
と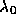 は行列Aの固有値である(今、縮退し
ている場合とかはちょっと置いておく。式は特別になるが振舞いはたいして変
わらない)。
固有方程式は
は行列Aの固有値である(今、縮退し
ている場合とかはちょっと置いておく。式は特別になるが振舞いはたいして変
わらない)。
固有方程式は

の形をとる。ここで、 としておく(抵抗が速度
と逆方向に働く)とすれば、k の値によって解の振舞いは5つの領域に分か
れる。
としておく(抵抗が速度
と逆方向に働く)とすれば、k の値によって解の振舞いは5つの領域に分か
れる。
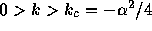 の時。固有値はどちらも負の実数である。
の時。固有値はどちらも負の実数である。
 で
で 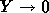 が任意の初期条件についてな
り立つ。つまり安定である。
が任意の初期条件についてな
り立つ。つまり安定である。
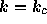 のとき。固有値が縮退し、解が
のとき。固有値が縮退し、解が 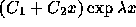 の形になる。安定。
の形になる。安定。
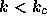 のとき。固有値は複素数だが、実部は負。安定。
のとき。固有値は複素数だが、実部は負。安定。
一般の微分方程式でも、定常解があればその回りで線形化することで同様な議 論ができることになる。安定であるということの条件は、全ての固有値の実部 が負であるということである。
なお、念のため注意しておくが、一般の場合には、複素固有値で実部が正とい
うばあいもありえる。上の例ではそれが起きなかったのは、 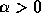 という条件をつけたからである。これを外す(負性抵抗)と、k<0 の時に振
動しながら平衡値から遠ざかっていく解が現れる(振動的発散)。
という条件をつけたからである。これを外す(負性抵抗)と、k<0 の時に振
動しながら平衡値から遠ざかっていく解が現れる(振動的発散)。