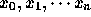 (ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を
(ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を  とす
る時、
とす
る時、 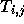 を以下のように定義する
を以下のように定義する
ここでやるのは、結局前回やった線形多段階法の場合と同様に、多項式補 間を作るということである。が、線形多段階法の場合とは違って、補間多項式 をもう一度積分するとかそういう必要はない。この時は、特別な計算法(ネヴィ ユのアルゴリズム)として知られる方法を使うことが出来る。
まず、一般的な場合についてネヴィユのアルゴリズムを示しておく。標本点
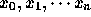 (ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を
(ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を  とす
る時、
とす
る時、 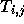 を以下のように定義する
を以下のように定義する

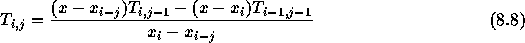
すると、一般に 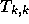 というのが、点
というのが、点  から
から  までを使った
k次補間多項式の x での値ということになる。特に、
までを使った
k次補間多項式の x での値ということになる。特に、  は全部
の点をつかった、もっとも精度が高いことが期待される近似値になる。
は全部
の点をつかった、もっとも精度が高いことが期待される近似値になる。
特に、 x= 0 のところでの値を求めるなら、上の式で x=0 とすればいい から、
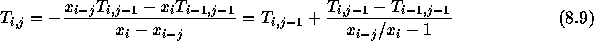
という形になる。
結局、表に示すように、左と左上の値から次のを計算できることになる。
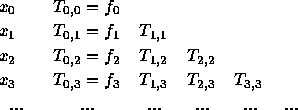
このやりかたで作った補間値が、 n 次まで正しいということは前回と同様 に証明できる。
この方法を使えば、任意の標本点数をつかっていくらでも高次の補間多項式を つくり、いくらでも高精度の近似値をえることができるということになる。こ のような、パラメータ h のいくつかの値で近似値を求め、その補間多項式 から h=0 での値を推測する方法のことを一般にリチャードソンの補外とい う。
なお、数値積分の話として考えると、積分 Sが

というように奇数次もあるような展開をもつならば、補間多項式は n 次に
しかならないが、台形公式のように偶数次しか持たない場合には 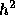 の多
項式として近似値を作ることができる。この時は次数が 2n次になることに
注意して欲しい。
の多
項式として近似値を作ることができる。この時は次数が 2n次になることに
注意して欲しい。