
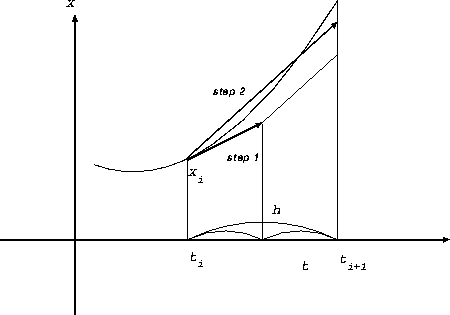
2次の Runge-Kutta 法とは、以下のようなものであった。

これについては、図的な説明というものが可能である。元の点からまずオイラー
法と同様に接線を引く。が、これを次の時刻まで延ばすのではなく、ステップ
の半分のところで止める。で、ここでもう一回微分方程式の右辺を評価する。
ここでの導関数の値を使って、もとのところ  から直線を引くわ
けである。
から直線を引くわ
けである。
実は、2次精度を実現する RK型の公式というのはこれ一つではない。以下のよ うなものも可能である。
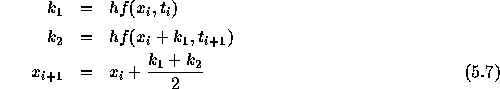
さらに、これらの公式を含む一般的な公式を与えることもできる。
もっと一般には、以下の形に書 くことができる。

自然数 s を段数(number of stages)という。  ,
,  ,
, 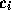 はパラメータであるが、a と c は普通
はパラメータであるが、a と c は普通

となるようにとる。これは、一般にそうでないような公式は不可能ではないが あまりいいことがない(精度がよくならない)からである。
と、こう、式に書いてしまうとすぐにはわからないが、例えば s=2の場合に 書き下してみると

と、まあ、こんな感じになる。こちらを良く見ればすぐにわかるように、
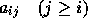 がすべて0ならば、
がすべて0ならば、 から順に計算していくこと
ができる。つまり、「陽的」公式になっている。
から順に計算していくこと
ができる。つまり、「陽的」公式になっている。
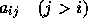 が0のときは、各
が0のときは、各  についての式に
についての式に 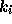 だ
けが入ってくる。これを半陰的 (semi-implicit) 公式という。この場合には、
まず
だ
けが入ってくる。これを半陰的 (semi-implicit) 公式という。この場合には、
まず 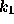 についての方程式をといて、次に
についての方程式をといて、次に 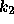 についてのを解いて、、、
と順番に計算出来る。
についてのを解いて、、、
と順番に計算出来る。
 に対する(一般には非線形な)方程式を一度に解く
必要がある。
に対する(一般には非線形な)方程式を一度に解く
必要がある。
前の後退オイラー法の場合と同様、なぜ陰的公式といった面倒なものをつくる かというのはよくわからないかもしれない。これについてはあとで説明すると して、まず、陽的公式の例について述べる。