 から出発した数値解が
から出発した数値解が  であったとし、また厳密
解が
であったとし、また厳密
解が 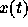 であるとする。これは、あくまでも
であるとする。これは、あくまでも  からの解---局所的な
解---であって、初期条件からの解ではないことに注意して欲しい。この時に、
数値解の局所離散化誤差が m次であるとは、
からの解---局所的な
解---であって、初期条件からの解ではないことに注意して欲しい。この時に、
数値解の局所離散化誤差が m次であるとは、
ここで、局所離散化誤差という概念を導入する。これは以下のように定義され
る。  から出発した数値解が
から出発した数値解が  であったとし、また厳密
解が
であったとし、また厳密
解が 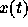 であるとする。これは、あくまでも
であるとする。これは、あくまでも  からの解---局所的な
解---であって、初期条件からの解ではないことに注意して欲しい。この時に、
数値解の局所離散化誤差が m次であるとは、
からの解---局所的な
解---であって、初期条件からの解ではないことに注意して欲しい。この時に、
数値解の局所離散化誤差が m次であるとは、

という関係を満たすこと、言い換えれば、ある定数Aが存在して、

なる関係を満たすことである。 Aは方程式に依存してよいが、hには依存しない必要がある。
なお、ある公式が m次の局所離散化誤差を持つ時、大域誤差は m-1次にな る。これは、先にやったオイラー法の一次収束の証明とまったく同様に行なう ことができる。従って、誤差について議論するには、とりあえず局所離散化誤 差がわかればいいということになる。
オイラー法の局所離散化誤差は、

と、 でのxの真の解のテイラー展開
でのxの真の解のテイラー展開
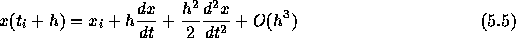
を比べてみればわかるように、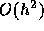 になっている。
になっている。
上に書いた方法はどうなっているかというのを考えると、少し計算すればわか
るように、  になっている。従って、局所で3次、大域誤差で2次にな
るわけである。
になっている。従って、局所で3次、大域誤差で2次にな
るわけである。
これは、例えば 1 次では必要な精度を実現するのに100万ステップ必要であっ たものが、大雑把にいってその平方根の 1000 ステップで済むということにな る。