一変数線形常微分方程式
を、前進（陽的）オイラー法
で積分する場合を考えてみる。すぐにわかるように、
から、
となる。安定であるとは 
で 
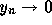と
なることであるから、その条件は
つまり
ということになる。
すこし考えてみるとすぐにわかるように、
の数値解は解とし
てはむちゃくちゃなものであるが、まあ、それでも安定ではある。
さて、多変数の場合はどうなるかということを考えると、結局、線形の場合は
対角化してしまえば一変数の場合と全く同じで、各変数が安定であればいい。
ただし、少し違うのは、複素数の固有値が発生するということである。このため
に、安定性条件が式(10.5)から簡単にならない。そこ
で、通常、 
とおいてこれがどういう範囲であれば安定
かという議論をする。
一変数（実固有値）の場合には、安定であるのは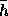
が開区間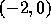 
にある場合である。複素数の固有値のときは、複素平面上で考えると、
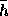が中心 
、半径 1 の円の
内部で安定ということになる。なお、上のような、元の方程式に安定解がある
時に数値解がそこにいくという性質を、特に「絶対安定性」ということがあり、
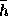の複素平面上で絶対安定である領域のことを絶対安定領域という。
前進オイラー法の絶対安定領域はあまり広くない。が、それが問題にならない
ような場合も結構多いということがわかるであろう。普通は h は
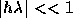となるようにとる。この時は、不安定になるのは固有値の虚
部が実部に比べて大きい場合に限られる。
