ここまでは、 Collisionless Boltzman 方程式から出発して、 Jeans の定理 を使って球対称な恒星系のモデルをいろいろ見てきた。これから2回程度、 Collisionless Boltzman 方程式のいろいろな平均(モーメント)をとること によって恒星系の性質を見ていくことにする。
まず、ジーンズ方程式を扱う。これは、形式としては流体の場合のオイラー方 程式、要するに運動方程式にあたるものである。導出は結構面倒なので少し丁 寧に進める。
Collisionless Boltzman 方程式は式11で与えら
れるが、これをまず速度空間全体で積分してみる。と、まず第3項は発散定理
によって表面積分に置き換えられ、
![]() の極限で
の極限で ![]() は
十分速く
は
十分速く![]() にいくので(普通は有限の
にいくので(普通は有限の![]() で0になってないと、自己重力的
にならない)、結局 0 になる。最初の2項は
で0になってないと、自己重力的
にならない)、結局 0 になる。最初の2項は
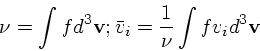 |
(12) |
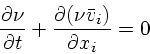 |
(13) |
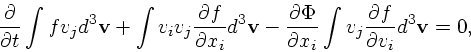 |
(14) |
さて、![]() について発散定理(1次元)を使えば
について発散定理(1次元)を使えば
 |
(15) |
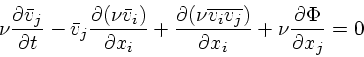 |
(17) |
| (18) |
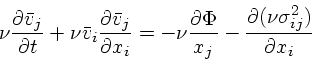 |
(19) |
これは、流体の場合のオイラー方程式(運動方程式)と大体同じ格好になって いる。左辺は平均の流れに沿ってみた平均速度の Lagrange 微分であり、右辺 第一項はポテンシャルから力である。
最後の項は普通なら圧力の項が出てくる。流体と違うのは、ここが非等方的な
stress tensor ![]() になっているということである。
になっているということである。
なお、いうまでもないが、速度分布が等方的であれば stress tensor は
![]() (
(![]() は単位行列)の形に書ける。さらに、等方的でない場合に
は、
は単位行列)の形に書ける。さらに、等方的でない場合に
は、
![]() は対称テンソルなので適当な座標系の回転により
対角化出来る。例えば
は対称テンソルなので適当な座標系の回転により
対角化出来る。例えば ![]() で書ける時には、一つの軸を原点に向けてと
れば対角化されるわけである。
で書ける時には、一つの軸を原点に向けてと
れば対角化されるわけである。
密度分布が球対称で平均の流れがない場合、極座標系での Jeans equation は以下の形に書き直せる:
![\begin{displaymath}
{d(\nu \overline{v_r^2}) \over dr} +
{\nu \over r} \left[2 \...
...+ \overline{v_{\phi}^2}\right)\right] = -\nu {d \Phi \over dr}
\end{displaymath}](img49.png) |
(20) |
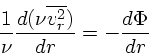 |
(21) |
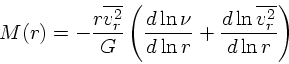 |
(22) |
ここで注意してほしいのは、 ![]() は質量を反映していないもの、例えば星の
数とか、あるいは単位体積あたりの luminosity の分布でも構わないというこ
とである。これは、もともとの Collisionless Boltzman 方程式は保存する量
であればなんでもなり立つからである。さらに、球対称、等方を仮定したので、表面
輝度分布や視線方向速度分布から輝度密度と速度分散の空間分布を求められる
ので、これらから「実際にどれだけの質量があるはずか」を求められるわけで
ある。これから、
は質量を反映していないもの、例えば星の
数とか、あるいは単位体積あたりの luminosity の分布でも構わないというこ
とである。これは、もともとの Collisionless Boltzman 方程式は保存する量
であればなんでもなり立つからである。さらに、球対称、等方を仮定したので、表面
輝度分布や視線方向速度分布から輝度密度と速度分散の空間分布を求められる
ので、これらから「実際にどれだけの質量があるはずか」を求められるわけで
ある。これから、 ![]() の空間分布が決まることになる。楕円銀河の中心に大
質量ブラックホールがあるというような話は、もっとも簡単にはこのようにし
て質量を推定する。
の空間分布が決まることになる。楕円銀河の中心に大
質量ブラックホールがあるというような話は、もっとも簡単にはこのようにし
て質量を推定する。
なお、逆に、![]() を一定として、速度の非等方性の空間分布を求めることも
できる。多くの、中心に大質量ブラックホールがあるとされている楕円銀河で、
非常に非等方性の高い速度分布を作れば観測された密度と速度分散の分布が説
明できないわけではないということが示されている。
を一定として、速度の非等方性の空間分布を求めることも
できる。多くの、中心に大質量ブラックホールがあるとされている楕円銀河で、
非常に非等方性の高い速度分布を作れば観測された密度と速度分散の分布が説
明できないわけではないということが示されている。
2002の9月に、球状星団 M15 の中心に太陽質量の 3000倍の質量のブラックホー ルを発見したという論文が発表され、 STScI がプレスリリースを大々的に行っ たので日本の新聞でも報道された。記憶にある人もいるかもしれない。
新聞発表はこんなの:
宇宙望遠鏡科学研究所のファン・デア・マレル博士が率いるチームは、ペガサス 座の方向、3万2千光年の彼方にある球状星団 M15 にブラックホールを発見し ました。彼の協力者で、やはり宇宙望遠鏡科学研究所のゲルセンは、ブラック ホールの質量が太陽の4000倍だということを突き止めました。
これまで、 X線での観測で .... 星形成銀河に非常に明るい X 線源が見つかっ ていました。これは中間質量ブラックホールとも解釈できるものでしたが、 他の解釈もできるものでした。これに対し、ハッブル(宇宙望遠鏡)による測定は、 個々の星の速度に基づくもので、直接ブラックホールの質量を与えるものです。
これは、ジーンズ方程式の利用のいろんな意味で教育的な例になっているので、 少し詳しく見ていこう。
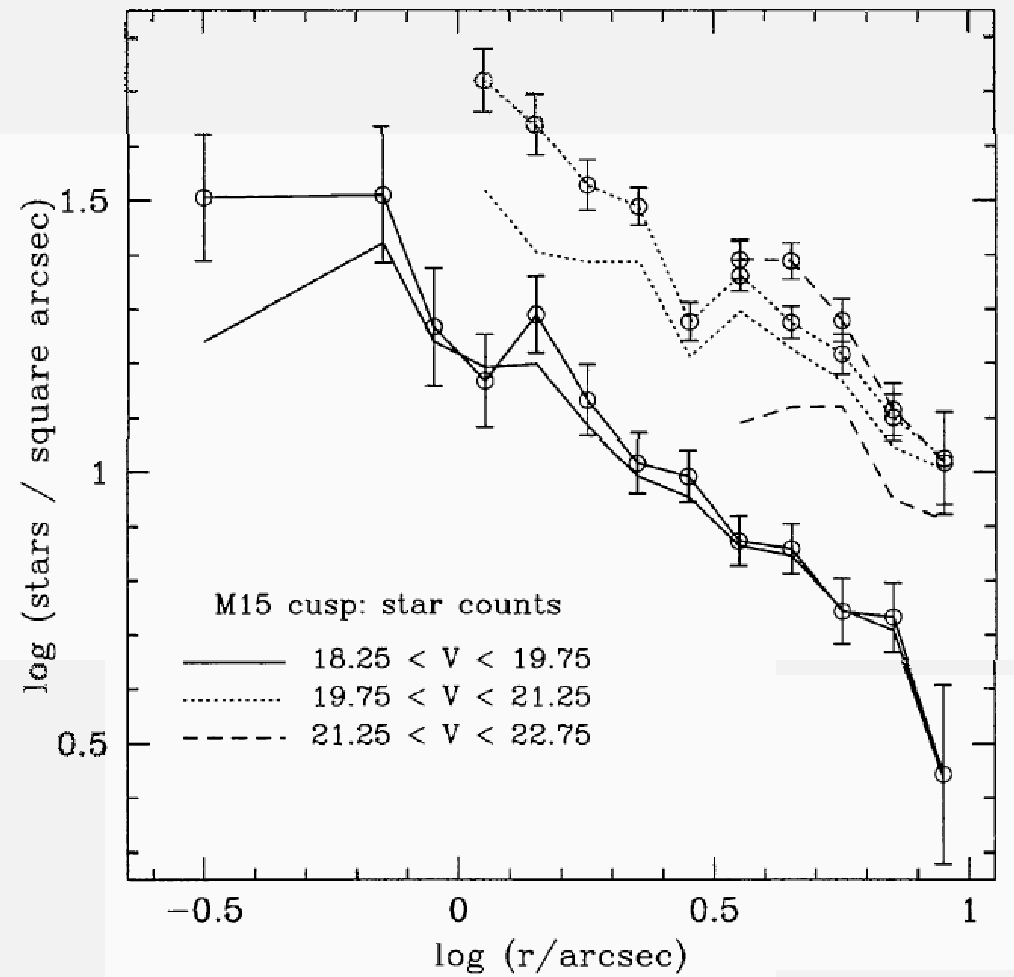
まず、観測はどういうものかというとこの図

が基本である。ハッブル宇宙望遠鏡の分光器を使って、球状星団の中心部のい くつかの星の視線速度を測定し、それから速度分散を求める。で、何故ブラックホールがあることになるかというと、下の図のような話である。
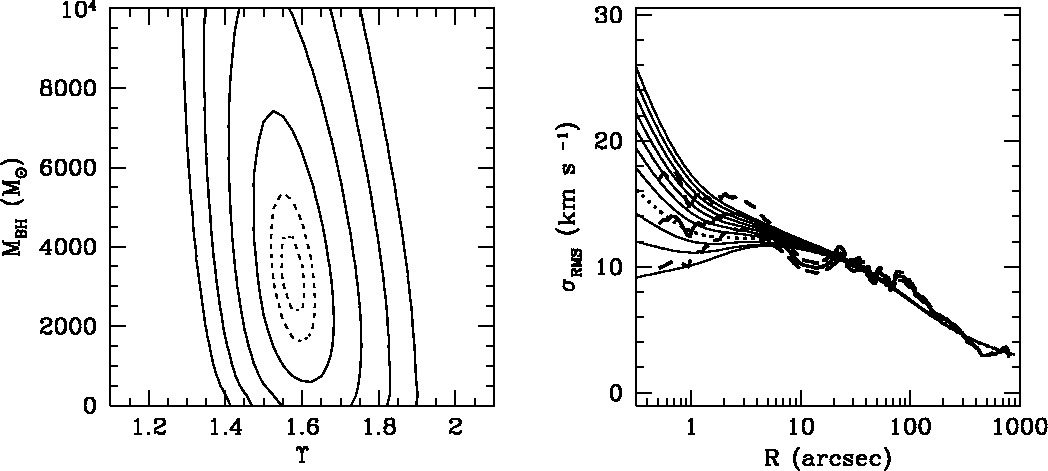
つまり、
まあ、今までに説明した通りの解析である。表面輝度はこんな感じである。
8.cm
 |
8.cm
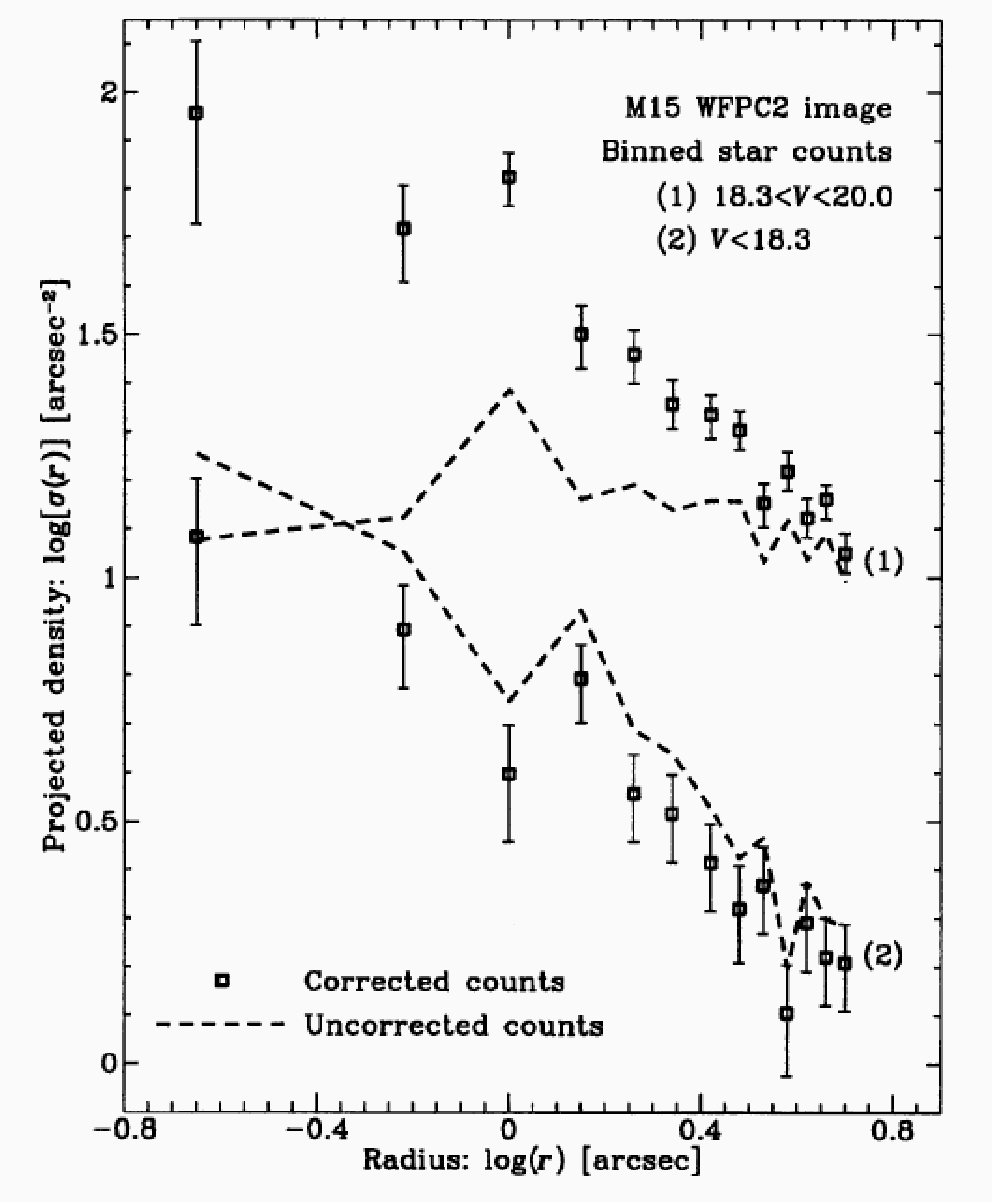 |
左: Sosin & King 1997, 右: Guhathakurta et al. 1996.
教科書通りの解析でブラックホールがあって論文になるならそれは結構なわけ
だが、この場合世の中はそんなに甘くない。何故かというと、球状星団では
(この講義の3-4回後ででてくる理由で)系が熱力学的に進化しており、 ![]() が一定という仮定が成り立たないからである。
が一定という仮定が成り立たないからである。
熱力学的な進化を簡単にいうと、星の系も普通のガスと同じようにエネルギー 等分配を成り立たせようと方向に局所的な速度分布が進化する。このため、速 度分散が初め同じだとすると、重い星は軽い星にエネルギーを与えて速度を小 さくしようとする。
ガスなら速度が小さくなって終わりだが、恒星系ではジーンズの定理というも
のがあるので話はそんなに簡単ではない。つまり、重い星が軽い星にエネルギー
を与えるということは、分布関数 ![]() が星の質量に依存するようになって、
重い星はエネルギーが低いところに動くということになる。
が星の質量に依存するようになって、
重い星はエネルギーが低いところに動くということになる。
これはつまり、エネルギーが低い、より中心近くを運動する軌道に移るという
ことである。つまり、星の質量分布がある恒星系が熱力学的に進化すると、重
い星が中心に集まってくる。球状星団では最も重い星は初期に大質量星が超新
星爆発してできた中性子星や、もうちょっと軽い星が進化してできた比較的重
い白色矮星であり、どちらも暗い。つまり、球状星団の ![]() が半径によら
ないと考えるのはかなり無理がある。というわけで、このブラックホールは怪しいのでは?と私を含めていろんな人が思った。
が半径によら
ないと考えるのはかなり無理がある。というわけで、このブラックホールは怪しいのでは?と私を含めていろんな人が思った。
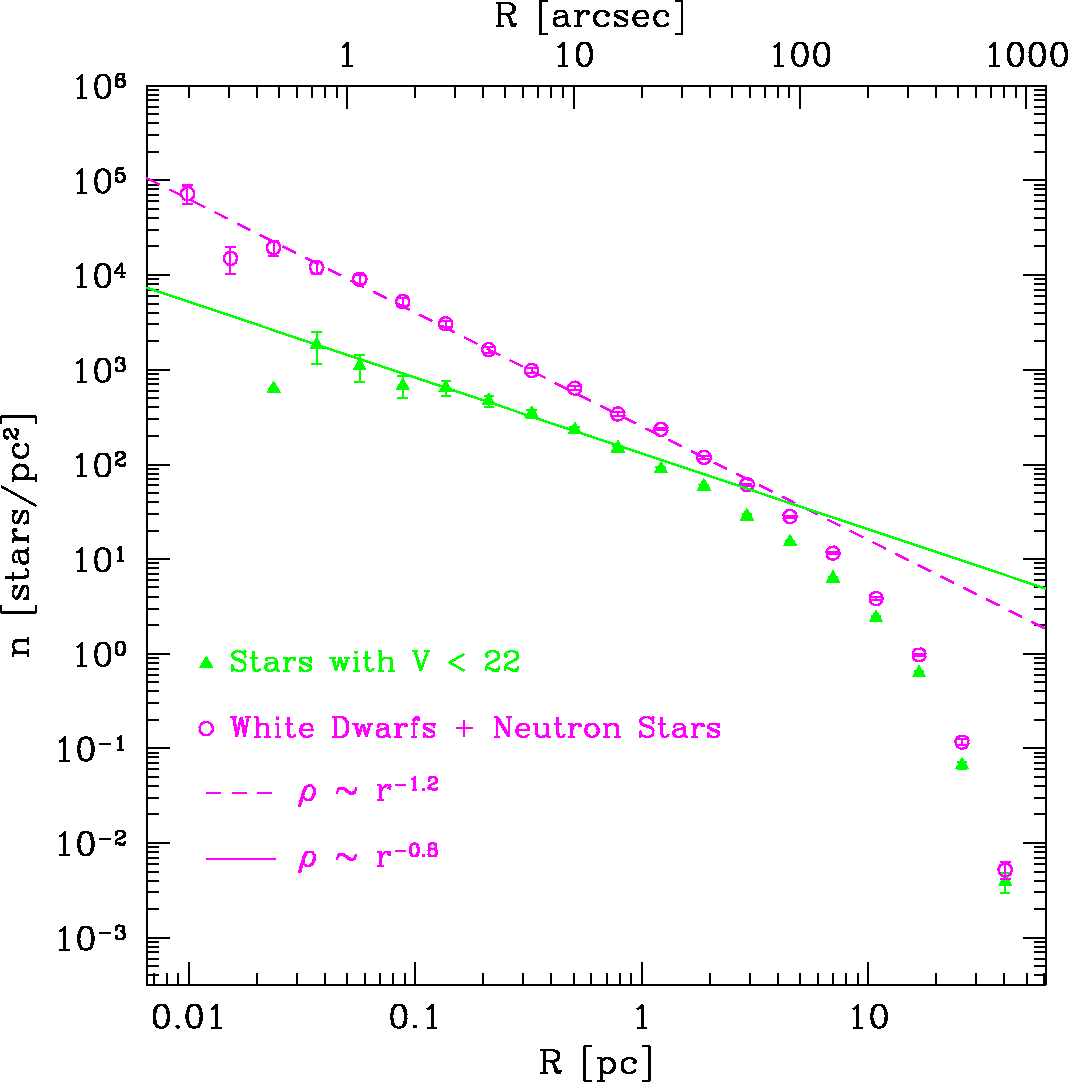
とはいっても、「間違ってるかもしれない」というだけでは人は納得しないの で、数値シミュレーションで球状星団を生まれた時から現在まで進化させて、 速度分散と輝度分布がどうなるか見てみることにした。 M15 は「コア崩壊型」 と呼ばれる、中心に向かってどこまでも密度が上がるタイプの星団なので、現 在ちょうどそのような密度(輝度)分布になるように初期条件を選んでみた。 星の質量分布とかは普通に太陽近傍の観測から示唆されているものを使う。
結果は Baumgardt et al., ApJ 2003, 582, L21 になって論文にしたわけだが、速度分散と輝度分布はそれぞれこんな感じになる。
8.cm
 |
8.cm
 |
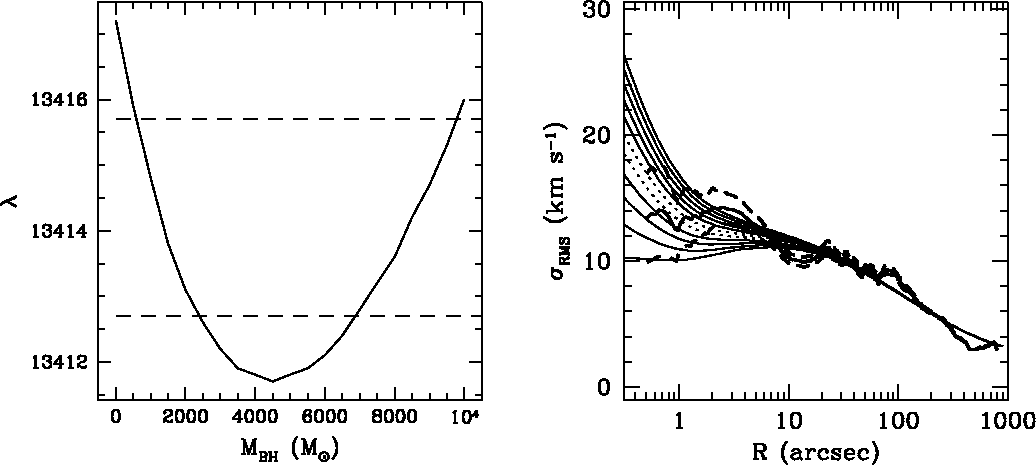
で、観測の人達と同じように ![]() 一定を仮定して解析すると
一定を仮定して解析すると
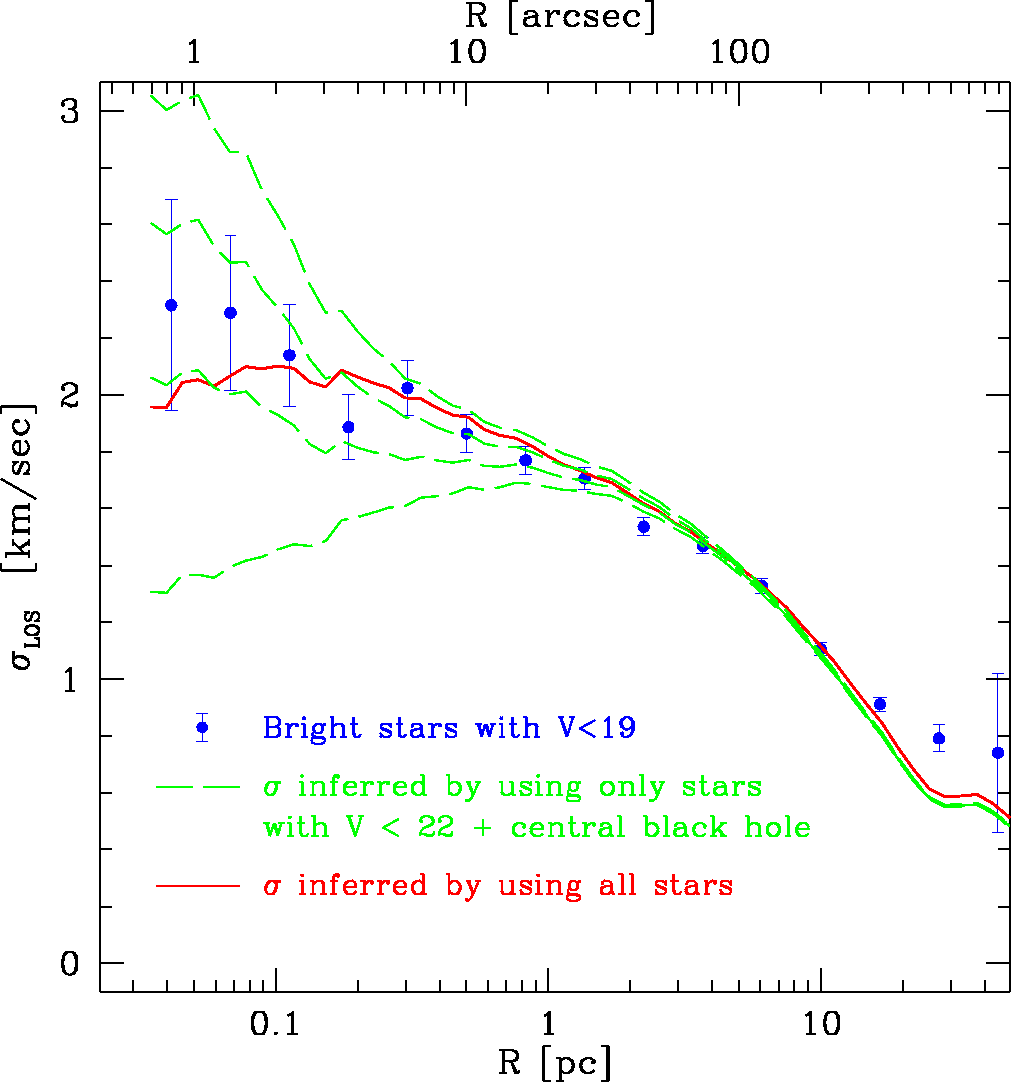
星だけでは中心で質量が足りなくて、ブラックホールが必要という結果になる。 モデル星団は M15 より軽いので、その分をスケールすると、大体 3000太陽質 量くらいのブラックホールがあるという結論になる。
まあ、そういうわけで、多分ブラックホールではなくて普通に熱力学的な進化 の結果中性子星等が中心に集まっているだけであろう。
という話で終わると、観測で論文書いた人が間抜けな感じがするが、実はもう
ちょっと話は複雑である。彼らは、 ![]() が一定ではない解析もしていて、
それは別の人(Dull et al. ApJ 1997)の、我々のと同じような数値シミュレーションの結果を使ったも
のであった。
が一定ではない解析もしていて、
それは別の人(Dull et al. ApJ 1997)の、我々のと同じような数値シミュレーションの結果を使ったも
のであった。
これであまり結果が変わらなかったから、彼らは安心して「ブラックホールが ある」という結果を発表した。しかし、これはおかしな話で、実は Dull et al. のモデル星団はハッブルのグループの解析より高い速度分散を与えていた。
7.8cm
 |
7cm
 |
使っている輝度分布は同じなので、同じジーンズ方程式と同じ ![]() プロファ
イルを使えば同じ速度分散が求まらないといけないのに、違う。
プロファ
イルを使えば同じ速度分散が求まらないといけないのに、違う。
これは実は、 Dull et al. の ![]() プロファイルのグラフが大嘘で、横軸が
3 倍間違っていたからだということが後で明らかになった。
プロファイルのグラフが大嘘で、横軸が
3 倍間違っていたからだということが後で明らかになった。

で、解析しなおすと、、、
15.5cm
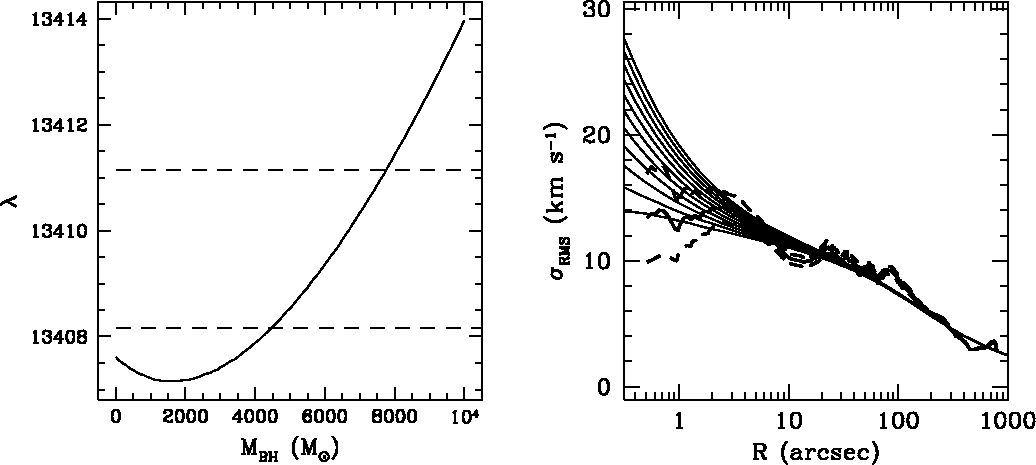
ブラックホールはなくてもいいという、真っ当な結果になってしまった。
この結果については、 STScI ではなく NASA HQ からプレスリリースがでている。
「ブラックホールがある」という結論を出した人達の解析方法には間違ったと ころがあったわけではないが、彼らが使った、他の人 (Dull et al.)の計算結果の論文のグラ フの1つの横軸が間違っていた。こんな間違いは避けようがない、と思うかも しれないが、この場合はそうでもない。というのは、 Dull et al. の理論モ デルの速度分散と、彼らが求めた速度分散がそもそもあってなかったので、 解析の過程のどこかに間違いがあるのは明らかだったからである。
まあ、最先端の、プレスリリースになるような研究でも、結構間違いというも のはある、というのが一つの教訓である。