非等方ということは、分布関数が ![]() の形で書けるということである。
まず、密度
の形で書けるということである。
まず、密度 ![]() がどう書けるかを考えてみよう。一般の分布関数で、密度
は単に
がどう書けるかを考えてみよう。一般の分布関数で、密度
は単に ![]() を速度空間全体で積分したもの
を速度空間全体で積分したもの
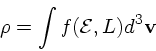 |
(1) |
| (2) |
 |
(3) |
一般に ![]() が
が ![]() に依存するしかたというのは無限にあるわけだが、以下、
そのなかで割と扱いやすいものとして、分布関数が
に依存するしかたというのは無限にあるわけだが、以下、
そのなかで割と扱いやすいものとして、分布関数が
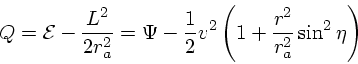 |
(4) |
まず、この Q の直観的な意味だが、 ![]() は
は
| (5) |
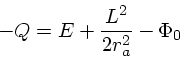 |
(6) |

この状況を図に示す。 E と L の平面で考えてみよう。まず、ポテンシャルが
与えられている時に、エネルギーを決めると角運動量は対応する円軌道の場合
に最大値になるので、分布関数は ![]() の線の左側でしか値をとらな
い。等方モデルの場合には、
の線の左側でしか値をとらな
い。等方モデルの場合には、 ![]() が
が ![]() に依存しないので、
に依存しないので、![]() の等高線は
水平線であるが、
の等高線は
水平線であるが、 ![]() が一定の線は赤で示した上に凸な放物線になる。
が一定の線は赤で示した上に凸な放物線になる。
Eが負の大きな値の場合(ポテンシャルの底に近い場合)
では、どうぜ ![]() の取り得る値の範囲が狭いので、実は等方的な場合とあま
り変わらない。これに対し、外側の
の取り得る値の範囲が狭いので、実は等方的な場合とあま
り変わらない。これに対し、外側の ![]() に近いところでは、等方の場合から
大きくずれる。例えば、元々の分布関数が
に近いところでは、等方の場合から
大きくずれる。例えば、元々の分布関数が
![]() まで値をもつ場
合でも、OM モデルの場合には原点から始まる等高線が
まで値をもつ場
合でも、OM モデルの場合には原点から始まる等高線が ![]() の限界になってそ
の右上では分布関数は 0 になるので、あまり角運動量の大きな粒子はないし、
エネルギーが 0 に近いほどとりえる角運動量の範囲は狭くなる。
の限界になってそ
の右上では分布関数は 0 になるので、あまり角運動量の大きな粒子はないし、
エネルギーが 0 に近いほどとりえる角運動量の範囲は狭くなる。
このような傾向は、例えば楕円銀河などの形成過程についてのいろいろなシナ リオで自然に起きること(そのうちに扱う)であり、理論的に調べられている 非等方モデルは大抵上のような角運動量でカットオフを持つようなモデルになっ ている。
なお、非等方性の重要な観測的応用として、楕円銀河の中心部の構造のモデル があるが、これについては後で時間があれば触れることにしたい。
上の密度の速度空間における積分を ![]() で
かきかえると
で
かきかえると
![\begin{displaymath}
\rho = 2\pi \int_0^{\pi}\sin \eta d\eta \int_0^{\Psi}f(Q)
{ \sqrt{2(\Psi - Q)} \over [1 + (r/r_a)^2\sin^2\eta]^{3/2}}dQ
\end{displaymath}](img20.png) |
(7) |
![\begin{displaymath}
\int_0^{\pi}{\sin \eta d\eta \over [1 + (r/r_a)^2\sin^2\eta]^{3/2}}
= {2 \over 1 + (r/r_a)^2}
\end{displaymath}](img23.png) |
(8) |