2 連星の役割

2.1 銀河系内連星

恒星系において、連星が特別な役割を果たすのは衝突系に限られる。その理由 は単純で、無衝突系では原理的に連星は単純にその合計の質量をもった星とみ なしてよいからである。

具体的な例として太陽系を考えてみる。もちろん太陽系は連星というわけでは ない(連星であるという話もあるがちょっと別の話である)。しかし、地球を始 めとする多数の惑星をもっている。その軌道周期は1年から数百年の程度であ り、典型的な連星とあまり変わらない。

太陽系の進化を考えるにあたっては、他の星との相互作用はそれほど重要では ない、ということになっている。実際問題として、太陽系ができてから現在ま での間に例えば地球の軌道半径くらいまで他の恒星が近づくようなことがあれ ば惑星の軌道は大きく乱されているはずで、現在のような 8 惑星が極めて平面 に近いところにいる、ということはありえない。

また、銀河円盤での太陽近傍の恒星の数密度、速度分散から実際に地球半径程 度まで他の恒星が近づくタイムスケールを計算することも可能である。

単位時間当りの遭遇確率は

$$P=n\sigma v$$

で与えられる。ここで $n$ は数密度、 $\sigma$ はここでは速度分散ではな く散乱断面積、 $v$ は相対速度である。

単位系として距離は $1{\rm AU}$, 時間は $1年$を単位とすると、速度は地球の軌道 速度が $2\pi$ となる。太陽系の周りの星の数密度を $1/{\rm pc^3}$ とし、 速度分散を 50km/s 程度とすれば、 $1{\rm pc} = 2\times 10^5{\rm AU}$ な ので

$$P \sim 10^{-15}$$

となり、宇宙年齢程度の間に他の星が近づく可能性は非常に小さい。

なお、この見積もりから、100AU 程度までなら他の恒星が近づく可能性がある、 ということもわかる。つまり、太陽系の場合、 TNO (海王星以遠天体)、特に その外側のほうや、 Oort cloud の進化を考える時には他の恒星との遭遇の影 響は無視できない。

2.2 球状星団

球状星団ではどうか、というのを考えてみる。

典型的な球状星団として、半径 5pc、質量 $10^6 M_{\odot}$ とすると密度は $10^4/{\rm pc^3}$ となり、速度分散は 10-20km/s と上の太陽系の見積もり よりも少し小さいので、 1AU 程度の連星ならば星団の外側のほうにあれば宇 宙年齢の間他の星と近接遭遇しないこともありえる。

逆にいうと、少し中心近く(密度は $1/r^2$であがるので)にあるとか、軌道長 半径が大きいとかだと、球状星団の中では連星は容易に他の星と相互作用する。

2.3 惑星形成過程

少し毛色の違う例として、惑星形成過程を考える。

現在の標準的な惑星形成モデル(いわゆる京都モデル)では、惑星は、ダストが 重力不安定や衝突で集まって成長する。この過程で連星ができたりしないか？ という話である。

標準的な惑星形成理論では、連星の形成は考慮されていない。その1つの理由 は、地球領域では(おそらく)あまり重要ではないからである。

連星が安定に存在できるためにはヒル半径の十分内側にいる必要がある。

(この辺もうちょっと説明必要)

具体的な式は適当な教科書をみて貰うとして、 Hill 半径の 1/2ないし 1/3 程度が安定性限界となる。これは、例えば地球の場合は 50万km 程度であり、 地球半径の 100倍以下である。

100倍というのは随分大きな差のようにも思えるが、連星形成過程を考えると そうでもない。

元々連星がないところで連星ができるプロセスは基本的に以下の2つである。

• 3 粒子の相互作用。大雑把にいうと、2つが近接遭遇しているところに もう1つがやってきて、その粒子の摂動によって2つが結合状態になる。

• 2粒子の非弾性相互作用。星同士であれば、潮汐変形するほど近くを通っ た結果、相対運動のエネルギーが内部運動に変換されて結合状態になる。

それぞれ、後でもう一度扱うが、とりあえず 3 粒子の相互作用の1例を:

9 cm

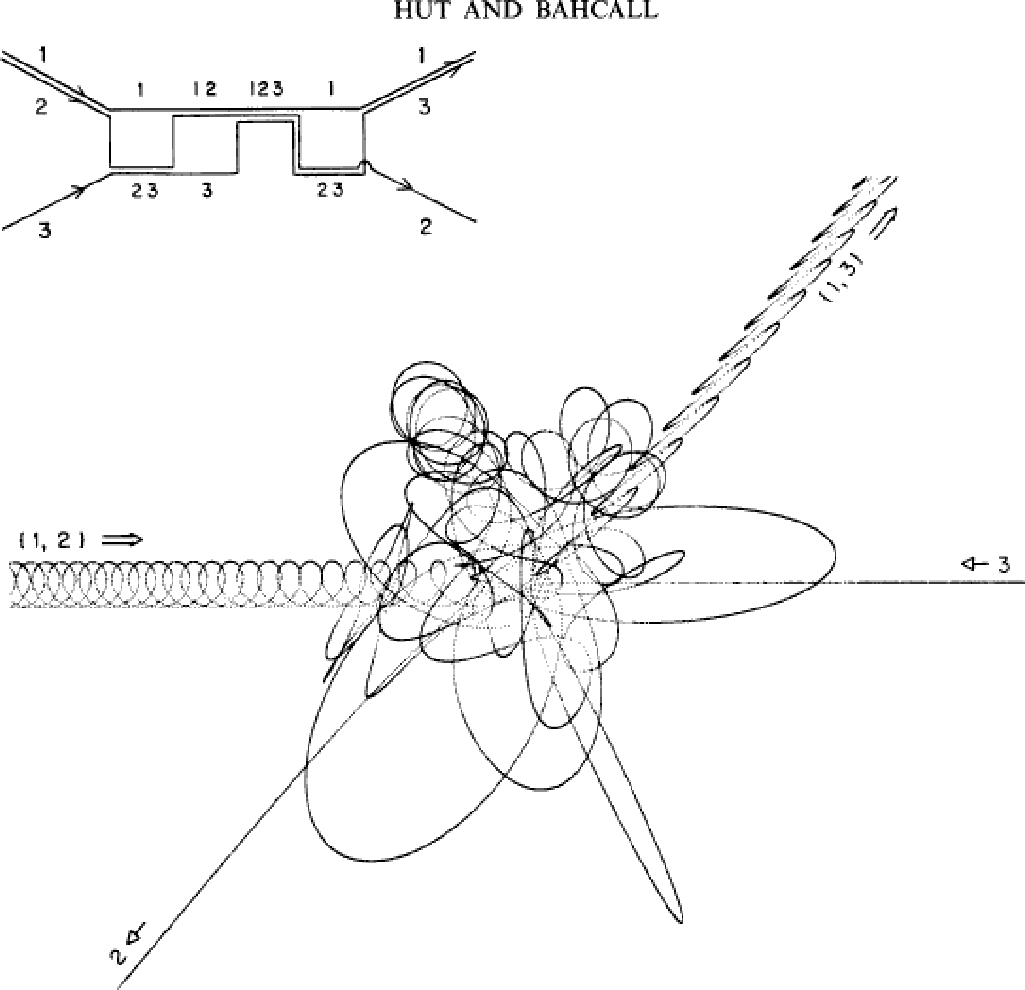
これは、円軌道の連星と、もうひとつの星の正面衝突の例である。複雑な相互 作用の結果、星の2番目と3番目が入れ替わって、元は円軌道だったのが離心率 が大きな連星になる。このようなので複雑な相互作用では、途中で2つの星が 近接遭遇することがあるし、また、途中で3つのうち1つがかなり遠くにいって しまうこともある。

つまり、元の連星の半径がヒル半径に比べて十分小さくないと、このような3 体相互作用の途中で一つがヒル半径の外側にいってしまうとか、あるいは衝突 するとかいったことが起こる。

このため、3体相互作用で連星ができたり、それが他の微惑星とさらに相互作 用するといったことは比較的重要ではないはず、と考えられている。

但し、実際にはこれまでの $N$体計算では惑星の物理半径を大きくして計算を 加速するテクニックが使われているので、本当のところがわかっているかどう かは不明である。