前回は、2体緩和のイメージとして、テスト粒子が、静止したバックグラウン ド粒子の分布の中を運動する場合を考えた。これで、テスト粒子が方向を変え るタイムスケールを導くことは出来たが、これだけでは「緩和」とはいい難い。
今日は、実際にバックグラウンドの粒子も動いている場合について考えること にする。
2体緩和によって、最終的には系が熱力学的に進化するわけであるが、これが 普通の流体(ガス)とは本質的に違うものであるということをここで再確認し ておこう。
ガスの場合、粒子の平均自由行程はシステムサイズよりもはるかに小さい。液 体であれば平均粒子間距離は粒子のサイズ程度であるし、気体であっても通常 の状況では考えている現象の空間スケールに比べて平均自由行程は小さい。ち なみに、非常に希薄な気体とか、あるいは本当に空間スケールの小さい現象で は平均自由行程が問題になる。これは例えば超高層での人工衛星の回りの気体 の流れとか、あるいは最近の磁気ヘッドの回りの空気の流れとかいったもので ある。
とにかく、通常のガスの場合、平均自由行程がシステムサイズより小さく、シ ステムサイズよりは小さく平均自由行程よりは大きいような空間スケールを考 えると、そのなかでほぼ熱平衡になっていると思っていいことになる。いいか えれば、いわゆる Local thermal equilibrium (LTE) の仮定が使える。こう なると、温度とか圧力とかいった量が近似的(といっても実際上非常に高い近 似精度で)に定義でき、そういったマクロな量で系の進化を扱う、特に熱の流 れを拡散方程式で書くということが可能になる。
しかし、自己重力質点系では状況が全くことなる。まず、粒子数が無限大の極 限では、平均自由行程も無限大であった。つまり、 LTE がなりたたないどこ ろか、そもそも熱平衡に向かう(すなわちエントロピーを生成する)ようなメ カニズムがなかったわけである。
粒子数が有限の場合も、依然として平均自由行程が長い、つまり、粒子数無限
大の時の軌道から、他の粒子との相互作用によって段々ずれていくわけだが、
そのずれる典型的なタイムスケールは ![]() 程度であった。
つまり、流体の場合とは全く逆に、ほとんど自由運動(というか、他の粒子全
体が作るポテンシャルに沿った運動)をしていて、その場が有限の粒子で表現
されるための揺らぎがあるので段々軌道が変わっていくということになるわけ
である。
程度であった。
つまり、流体の場合とは全く逆に、ほとんど自由運動(というか、他の粒子全
体が作るポテンシャルに沿った運動)をしていて、その場が有限の粒子で表現
されるための揺らぎがあるので段々軌道が変わっていくということになるわけ
である。
従って、ローカルな熱平衡を仮定して拡散係数/輸送係数を求めるというのと は逆に、ある一つの粒子が系の中を動き回りながらどういうふうにエネルギー 等を変化させていくかという観点で見ていくことになる。
これをすこし別ないい方をすれば、通常の空間のなかでの密度や温度の変化を 考える代わりに、また6次元位相空間のなかでの分布関数の進化を考えるとい うことに当たる。具体的には、これまで無視してきた「衝突項」というものを ちゃんと評価して、どういうものかみてやろうということである。
さて、以下ではバックグラウンドの粒子分布のもとでの一つのテスト粒子の振 舞いを考える。先週と違うのは、バックグラウンドも動いていることと、テス ト粒子も有限の質量を持つことである。バックグラウンドの粒子は一様に分布 するものとし、ある速度分布に従うとする。さらに、バックグラウンドの粒子 間の相互作用とかは考えないことにする。これで本当にいいかどうかはちょっ と良くわからない問題であるが、まあ、とりあえずやってみることにしよう。
前回と同じく、分布している質点の質量
を ![]() 、数密度を
、数密度を ![]() とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ)
とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ) ![]() を相対速度
を相対速度
![]() で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
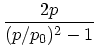 |
|||
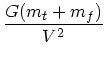 |
(1) |
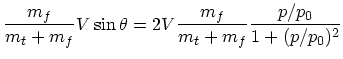 |
(2) | ||
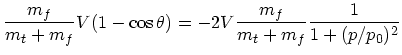 |
(3) |
| (4) | |||
 |
(5) | ||
 |
(6) |
| (7) |
上の式で、
![]() の項は先週扱った角度の曲がる項と同じも
のである。先週の話と違うのは、ネットに速度が小さくなる成分がある、すな
わち
の項は先週扱った角度の曲がる項と同じも
のである。先週の話と違うのは、ネットに速度が小さくなる成分がある、すな
わち
![]() が負で有限の値をもつということである。
が負で有限の値をもつということである。
これは、実は2回前(だっけ?)にやった dynamical friction そのものであ
る。つまり、回りが止まっているなかを粒子が走っていくと、それが回りを引っ
張って動かすので、その分エネルギーを失って段々速度が落ちるわけである。
これは、 ![]() が大きい(
が大きい(![]() が小さい)極限では
が小さい)極限では ![]() 、つまり質量
密度によっていて、バックグラウンドの粒子の質量に依存しないことに注意し
てほしい。これに対し、他の項は
、つまり質量
密度によっていて、バックグラウンドの粒子の質量に依存しないことに注意し
てほしい。これに対し、他の項は![]() に比例していて、質量密度が同
じでも粒子の質量が大きいほうが値が大きくなるのは先週にやった通りである。
に比例していて、質量密度が同
じでも粒子の質量が大きいほうが値が大きくなるのは先週にやった通りである。
さて、ここではとりあえず1次と2次の項を求めたわけだが、それより先の項に ついては考えなくてもいいのだろうか?ここでは粒子の軌道変化がたくさんの 散乱のランダムな重ね合わせで書けるとした。この仮定が正しければ、たくさ ん散乱を受けた後の速度の分布は1次と2次のモーメントで決まるガウス分布に なり、従って3次より高いモーメントの寄与は考えなくてもいいことになる。
問題はこの仮定が正しいかどうかであるが、実は理論的にはそれほど正確なわ
けではない。というのは、インパクトパラメータが例えば ![]() の程度の散
乱というのも現実におき、その効果はそれ以外の散乱すべての寄与に比べてせ
いぜい
の程度の散
乱というのも現実におき、その効果はそれ以外の散乱すべての寄与に比べてせ
いぜい ![]() 程度でしか小さくないからである。まあ、しかし、そ
んなことをいっていても高次の項があっては計算出来ないし、とりあえず
程度でしか小さくないからである。まあ、しかし、そ
んなことをいっていても高次の項があっては計算出来ないし、とりあえず
![]() 程度で小さいということも確かなので、以下高次のモーメン
トは考えない。
程度で小さいということも確かなので、以下高次のモーメン
トは考えない。
というわけで、いよいよバックグラウンドが動いている場合ということになる。 この時でも、相対速度の変化自体は前節に述べたもので正しいが、相対速度に フィールド粒子の速度成分が入ってくることになる。
以下、二種類の単位ベクトル系をとって、その上で考える。一つは
![]() であり、元の空間に固定されている。もう一つは
であり、元の空間に固定されている。もう一つは
![]() であり、最初の成分を相対速度
であり、最初の成分を相対速度
![]() に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
まず、1次の項は相対速度に平行な成分だけであった。このことから、ある方
向の速度変化は
| (8) |
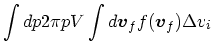 |
(9) | ||
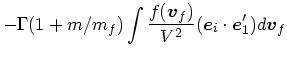 |
(10) |
さて、2次の項についてであるが、前節で見たように
![]() に垂直な成分、す
なわち
に垂直な成分、す
なわち
![]() と
と
![]() の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
| (11) |
| (12) |
| (13) |
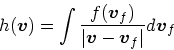 |
(14) |
| (15) |
2次の項についても同様な整理が可能である。![]() は
は
![]() ,
,
![]() の
の
![]() と
と
![]() によって張られる平面への写像の内積なので、
によって張られる平面への写像の内積なので、
![]() と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
| (16) |
 |
(17) |
| (18) |
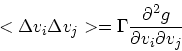 |
(19) |
前節では、バックグラウンドの速度分布が任意のものについて、実際に計算可 能な式を導いた。ここでは、速度分布が等方的な場合につ いて式を単純化してみる。
速度分布が等方的な場合、![]() や
や![]() の積分を、
の積分を、
![]() の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
![]() と
と
![]() の
なす角度を
の
なす角度を ![]() とし、
とし、
![]() とすれば、球面上での積分
が、まず
とすれば、球面上での積分
が、まず![]() については
については
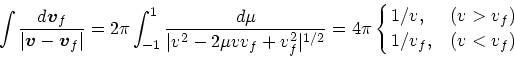 |
(20) |
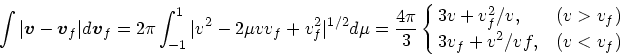 |
(21) |
 |
|||
 |
(22) |
![$\displaystyle {4\pi v^3 \over 3} [3F_2(v) + F_4(v) + 3E_3(v) +E_1(v)]$](img81.png) |
(23) |
これらから、最終的な結果、すなわち、バックグラウンドが動いている時の、
速度に平行な速度変化と垂直なそれを書き下せることになる。それらは、結局、
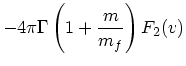 |
(24) | ||
![$\displaystyle {8 \pi \Gamma v \over 3} [F_4(v) + E_1(v)]$](img83.png) |
(25) | ||
![$\displaystyle {8 \pi \Gamma v \over 3} [3F_2(v)-F_4(v) + 2NE_1(v)]$](img84.png) |
(26) |
| (27) |
![\begin{displaymath}
<\Delta E> = 4 \pi \Gamma v\left[E_1(v) -{m \over m_f}F_2(v)\right]
\end{displaymath}](img87.png) |
(28) |
| (29) |
さて、速度分布を熱平衡、すなわち
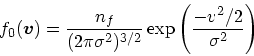 |
(30) |
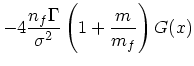 |
(31) | ||
 |
(32) | ||
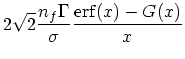 |
(33) | ||
![$\displaystyle \sqrt{2}{n_f \Gamma\over \sigma }\left[-{m \over m_f}{\rm erf}(x)
+ \left( 1 + {m \over m_f}\right)x {\rm erf}'(x)\right]$](img95.png) |
(34) |
| (35) |
山ほど式はでてきたものの、全然なんだかわからないという気分になった人も まあいるのではないかと思うので、以下、上の式の意味についてちょっと考え てみよう。
まず、速度の1次の項を見てみる。これは、速度分布には![]() だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、
だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、 ![]() が大きい極限では
が大きい極限では
![]() となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、
となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、![]() が小さい極限では、
が小さい極限では、![]() を一定と見なすことが
出来るので
を一定と見なすことが
出来るので ![]() となる。
となる。
これは、タイムスケールを考えてみると、速度が大きい極限では減速のタイム
スケールが ![]() であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
これに対し、速度が小さいほうではタイムスケールがある一定値、つまりは
![]() で決まる値あたりになるということである。
で決まる値あたりになるということである。
この1次の項は、前に述べたように dynamical friction を表している。これ が問題になる場面は、例えば恒星系が質量の違う2つの成分から出来ているよ うな場合である。力学平衡で、分布関数に質量依存がないようなものを考える と、これは熱平衡から遠くはなれている。従って、上の式で決まるタイムスケー ルで重いものがエネルギーを失い、軽いものがエネルギーを得る。
なお、、自己重力系ではこのエネルギー交換の結果熱平衡に向かうとは限らな いということに注意する必要がある。つまり、重いものがエネルギーを失い、 軽いものがエネルギーを得るということは、それぞれの分布関数が変わり、空 間分布も変わるということである。具体的には、重いものは中心に落ちるし、 軽いものは外側に押し出される。
さて、次に、2次の項を見てみる。速度に平行な成分も垂直な成分も、 ![]() が
大きい極限では0にいく。特に、 垂直な成分は
が
大きい極限では0にいく。特に、 垂直な成分は![]() に反比例する。これに対し、
速度が
に反比例する。これに対し、
速度が![]() の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。
の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。