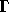4 Ritz-Galerkin法

弱形式や変分問題にしても、それだけでは元の方程式以上にどうやって解けば いいかわからない。しかし、近似的（数値的）に解こうというときには、これ らの形式から具体的な解を構成できる。

もとの弱形式では、 u や v の範囲は実ヒルベルト空間（境界 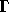で 0 とか微分可能性がどうとかややこしい条件はつくが）である。ヒルベルト空 間というのは何だったか忘れたとか知らないとかいう人がいるかもしれないが、 要するに内積が定義できるベクトル空間のことである。元が関数だと、次元は 無限ということになるが、まあ、そういうものである。

ここで、近似解を求めようという作業は、無限次元ヒルベルト空間を適当な有 限次元に制限して、その範囲で解こうということであると思いなさいというの が、基本的なRitz-Galerkin法の精神である。この有限次元部分空間を以下 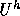と書くことにする。有限次元に制限する方法はいろ いろありえるが、もちろんそのとり方によってどれくらいまともな答がでるか というのは変わってくる。ここで、弱形式の時に u だけでなく v も同じ 部分空間に制限してしまうのがミソで、これで自由度の数と方程式の数を合わ せることができる。

もっとも、それで方程式を解いたとして、求まった解がもともとのポアソン方 程式の近似解に本当になっているかどうかというのは全然自明ではない。が、 これをやってるとそれだけでこの講義半年分が終るので、その議論は省略する ことにしたい。

以下、まず、形式的にどうやって解が求められるかということを考える。 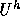は有限次元線形空間なので、基底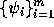がとれて、 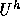の任意の元は 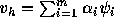と書ける。但 し、ここで 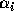は実数係数である。

もとの弱形式は

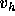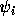であった。 ここで考えるa, F はどちらも線形汎関数（作用素、演算子、、、 この辺の言葉の使い方は業界によって違うような気がする）なので、これが制 限された部分空間で可能な任意の についてなり立つということは、各 基底 について、

がなり立つというのと同じことである。で、さらに 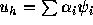と書けることから、これは結局 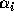についての連立1次方程式

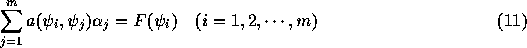
あるいは、例によって行列を使って

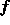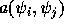と書けることになる。A や の要素 と 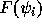を計算して具体的に A と 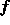を決めれば、上の方程式を 解くことで 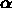が求まり、近似解 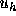が求まるわけである。