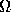 は有界開区間なので、適当な変数変換をして
単位開区間
は有界開区間なので、適当な変数変換をして
単位開区間 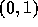 であると思っていい。ここでの近似関数空間としては、
例えばフーリエ級数 (sin 級数) を有限項で打ち切ったものが考えられる。こ
の時は、基底が直交基底で、結局
であると思っていい。ここでの近似関数空間としては、
例えばフーリエ級数 (sin 級数) を有限項で打ち切ったものが考えられる。こ
の時は、基底が直交基底で、結局 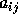 が対角要素以外は 0 になるの
で右辺の積分ができれば答が求まる。
が対角要素以外は 0 になるの
で右辺の積分ができれば答が求まる。
さて、近似関数としてはどんなものがあり得るかの例をちょっとだけあげる。
空間1次元だと、領域 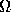 は有界開区間なので、適当な変数変換をして
単位開区間
は有界開区間なので、適当な変数変換をして
単位開区間 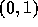 であると思っていい。ここでの近似関数空間としては、
例えばフーリエ級数 (sin 級数) を有限項で打ち切ったものが考えられる。こ
の時は、基底が直交基底で、結局
であると思っていい。ここでの近似関数空間としては、
例えばフーリエ級数 (sin 級数) を有限項で打ち切ったものが考えられる。こ
の時は、基底が直交基底で、結局  が対角要素以外は 0 になるの
で右辺の積分ができれば答が求まる。
が対角要素以外は 0 になるの
で右辺の積分ができれば答が求まる。
が、まあ、2次元以上の話というか、有限要素法の話につなげるために、まず
折れ線関数というものを考える。これは、区間のなかに適当な分点 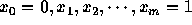 を考えて、各分点の間で1次関数、各分点では連続
になるような関数である。これは、基底関数として、図に示すような、各
を考えて、各分点の間で1次関数、各分点では連続
になるような関数である。これは、基底関数として、図に示すような、各
 のところで 1、その両側の分点で 0 になるような区分的1次関数を
考えるということに相当する。
のところで 1、その両側の分点で 0 になるような区分的1次関数を
考えるということに相当する。
この場合には、フーリエ級数の場合と違って基底が直交していないので、左辺
は対角行列にはならない。しかし、一つ向こうの基底とは直交しているので、
A は3重対角行列になる。左辺の評価には一階微分が必要だが、これはもち
ろん定数関数で簡単に計算できる。右辺の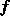 のほうは1次のままだが、こ
れも簡単に評価できる。
のほうは1次のままだが、こ
れも簡単に評価できる。
例えば、分点が等間隔の場合を考えてみると、折れ線基底から出てくる方程式
は結局2次の差分近似と同じになる。それではなにも変わらないではないかと
思うかもしれないが、実はそうではない。というのは、今使っている折れ線基
底は、分割が等分割である必要が全くないからである。どのように分点をとっ
てきても、A や 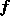 は機械的に計算できる。
は機械的に計算できる。
まあ、1次元であれば差分式を中心差分を拡張して定義できるので、それほど ありがたみが見えないのは確かであろう。
この場合は、まず分割をどうするかが問題である。とりあえず、2次元として 広く使われている3角形分割を考える。ここで、どの3角形の頂点も、他の3角 形の辺の途中に来たりすることはないように分割することにする。すると、折 れ線関数を自然に拡張したものとして、各3角形の中では平面(1次関数)であ るような関数を考えることができる。ちなみに3次元でも話は同じで4面体にす ればいい。この時は、結局基底関数として、ある節点(三角形の頂点)で1、 それにつながった他のすべての頂点で0になるような多角錐を考えることにな る。
有限要素法の強力さは、多次元の場合により明らかである。つまり、空間を3 角形分割しただけでは、2階の導関数なんてものがいったいどうやって構成で きるかは良くわからないので、差分式自体のたてようがない。しかし、有限要 素法では、元の微分方程式を積分型の方程式に書き直すことで、空間が分割さ れていれば必ず近似解を構成できるわけである。