ポアソン方程式
のディリクレ問題（境界で関数値を与えるもの。面倒なので関数値は 0 とす
る）を考える。記号を簡単にするため、方程式を解くべき領域を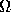 
、
境界を 
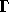と書くことにしよう。
領域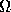 
は一般には N次元ユークリッド空間 
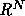の有界で連結な
開部分集合ということにする。開集合なのは、単に境界上では微分が定義できない
ので微分方程式もなりたたないからである。
ここで、天下りではあるが、任意の関数 v (ただし、境界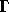 
上で
は 0 )を考えて、これを元のポアソン方程式の両側に掛けて積分すると、もち
ろん
である。ここで Green の公式
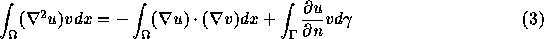
（ここで n は境界での外向き単位法線である）と、境界で v=0 という仮 定から、
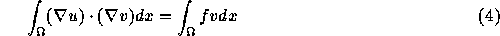
というふうに書き直せる。
この形式のことを弱形式という。ここで弱というのは、 元のポアソン方程式の解は、もちろん任意の v に対してこの方程式を満た しているのに対し、任意の v に対して弱定式化をみたす関数 u がもと の方程式の解かどうかというのはそんなに自明ではない、例えば、2階微分が 存在しなくても弱形式の解ではありえるかもしれないというようなことがある からである。
ここではポアソン方程式のディリクレ問題だけを考えるが、もっと一般に波動 方程式や流体の方程式でもこのような弱形式を導くことが、いろいろ工夫する とできる。