

Next: About this document ...
Up: 7 常微分方程式の数値解法:初期値問題
Previous: 1 Euler 法とRunge-Kutta 法
Subsections
常微分方程式の初期値問題の例として、ポリトロープガス球のLane-Emden方程式を解
いてみよう。
恒星の内部構造の釣り合いを考えよう。
- 静水圧平衡
- 連続の式
- 状態方程式
- エネルギー輸達
- 吸収係数
- 吸収係数は、ガスの成分と状態による。
 |
(42) |
- エネルギー保存式
- 核反応生成率
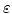 は、エネルギー発生率を表す。星のエネルギー源は核反応である。これは、
ガスの成分と状態によって決まる。
は、エネルギー発生率を表す。星のエネルギー源は核反応である。これは、
ガスの成分と状態によって決まる。
 |
(44) |
状態方程式
 |
(45) |
において、
 |
(46) |
として解く事を考える。これを指数  のポリトロープと呼ぶ。
すると、上の基礎方程式で、力学平衡を表す
静水圧平衡の式と連続の式の二本の式がエネルギーの式と分離する。
即ち静水圧平衡の式より
のポリトロープと呼ぶ。
すると、上の基礎方程式で、力学平衡を表す
静水圧平衡の式と連続の式の二本の式がエネルギーの式と分離する。
即ち静水圧平衡の式より
 |
(47) |
を得、これを連続の式に代入すれば
 |
(48) |
を得る。
ここで
 |
(49) |
( は 星の中心密度)
として、先の状態方程式を仮定すると
は 星の中心密度)
として、先の状態方程式を仮定すると
 |
(50) |
を得る。
![\begin{displaymath}
\alpha \equiv \left[
{{(N+1)K}\over{4\pi G}} \rho_{\rm c}^{{{1}\over{N}}-1}
\right]^{1/2}
\end{displaymath}](img146.png) |
(51) |
で 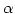 を定義し、
を定義し、
 |
(52) |
で 無次元変数  を導入すると
を導入すると
 |
(53) |
を得る。これを 指数  の Lane-Emden equation と呼ぶ。
の Lane-Emden equation と呼ぶ。
星の中心  で
で
 |
(54) |
 |
(55) |
である。また  になる点が星の表面に相当する。
になる点が星の表面に相当する。
Lane-Emden 方程式 (7.35) は、 が、確定特異点になっている。
この様な場合、特異点の近傍での解のLaurent級数展開を考える必要がある。
いま、
が、確定特異点になっている。
この様な場合、特異点の近傍での解のLaurent級数展開を考える必要がある。
いま、 のまわりの形式解を
のまわりの形式解を
 |
(56) |
の形に仮定して、(7.35)式の両辺に代入すれば、左辺は、
 |
(57) |
一方、右辺は、
 |
(58) |
となる。 両辺の と
と の係数を比較して、
の係数を比較して、
 ,
, を得る。よって、中心近傍での解は、
を得る。よって、中心近傍での解は、
 |
(59) |
と表される。
例えば、 ,
,
 とおくと、
(7.35)式は次の二元連立一階微分方程式となる:
とおくと、
(7.35)式は次の二元連立一階微分方程式となる:
 |
(60) |
 |
(61) |
この方程式を、 から外側に向かって、Runge-Kutta法で積分していけば良い。
中心は、明らかに確定特異点だから、初期値は、
から外側に向かって、Runge-Kutta法で積分していけば良い。
中心は、明らかに確定特異点だから、初期値は、 ではなく、中心からわずかに
ずれた
ではなく、中心からわずかに
ずれた で設定する。そこでの
で設定する。そこでの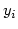 の値は、上で求めた展開から得られる
の値は、上で求めた展開から得られる
 |
(62) |
 |
(63) |
を使って求める。
積分を進めて、 になる点が表面である。その
になる点が表面である。その を
を とすると、
星の半径は
とすると、
星の半径は
となる。
中心から より内側に含まれる質量は
より内側に含まれる質量は
或いは、(7.35)式を使って書き直すと、
で与えられる。従って、星の全質量は
![\begin{displaymath}
M = -4\pi\left[{{(N+1)K}\over{4\pi G}}\right]^{3/2}
\rho_{\...
...3-N)/2N}
\left(\xi^2{{d\theta}\over{d\xi}}\right)_{\xi=\xi_1}
\end{displaymath}](img180.png) |
(67) |
となる。
- 指数
 、
、 、及び
、及び  の場合について、Lane-Emden equation を Runge-Kutta 法を用いて数値的に解け。
の場合について、Lane-Emden equation を Runge-Kutta 法を用いて数値的に解け。
- 太陽が
 のポリトロープで近似できるとして、その内部構造を求めよ。
但し太陽半径
のポリトロープで近似できるとして、その内部構造を求めよ。
但し太陽半径
 km、
太陽質量
km、
太陽質量
 kg
とし、内部は完全気体の状態方程式
kg
とし、内部は完全気体の状態方程式
 |
(68) |
に従うものとする。
ここで は単位体積当たりの全粒子数、
は単位体積当たりの全粒子数、 はボルツマン定数。
今、水素、ヘリウム、それ以外の元素が質量比
はボルツマン定数。
今、水素、ヘリウム、それ以外の元素が質量比  である
完全電離理想気体を考える。水素原子の質量を
である
完全電離理想気体を考える。水素原子の質量を  で表わすとすると、
水素については核の数密度は
で表わすとすると、
水素については核の数密度は
 、電子の数密度は同じく
、電子の数密度は同じく
 、ヘリウムについては核の数密度は
、ヘリウムについては核の数密度は
 、
電子の数密度は
、
電子の数密度は
 、それら以外の元素については、それぞれの
元素の atomic weight を
、それら以外の元素については、それぞれの
元素の atomic weight を  、atomic number を
、atomic number を  とすると、
核の数密度は
とすると、
核の数密度は
 、
電子の数密度は
、
電子の数密度は
 だから、
全粒子数
だから、
全粒子数  は
は
 |
(69) |
となる。
重元素については
 だから、
水素とヘリウム以外の元素の質量比を
だから、
水素とヘリウム以外の元素の質量比を
 と表わす事にすれば、
と表わす事にすれば、
 |
(70) |
であり、ガス圧は
ここに は
は
 |
(73) |
で、平均分子量と呼ぶ。また
 J
J kg
kg K
K 。
(
。
(
 J
J K
K 、
、
 kg)。
太陽の水素、ヘリウム、金属の質量比はそれぞれ
kg)。
太陽の水素、ヘリウム、金属の質量比はそれぞれ
 、
、 、
、 とする。
とする。
- 白色矮星の内部では、電子は縮退し、その縮退圧が星を支えるようになる。
電子が完全に縮退した場合、
分布関数は
 |
(74) |
全電子数 は
は
 |
(75) |
だから、与えられた電子数に対しては  は
は
 |
(76) |
 であれば、
であれば、
 として、電子の縮退による圧力は
として、電子の縮退による圧力は
となり、 のポリトロープに相当する。
ここで、
のポリトロープに相当する。
ここで、
 。
白色矮星の状態方程式を(7.60)式とした時、その半径と質量はどれぐらいにな
るか。中心密度は
。
白色矮星の状態方程式を(7.60)式とした時、その半径と質量はどれぐらいにな
るか。中心密度は
 を目安とせよ。
また、半径の質量依存性はどうなるか。
を目安とせよ。
また、半径の質量依存性はどうなるか。
相対論的縮退の場合は、
となる。
状態方程式が(7.60)式で表される程の高密度の白色矮星では、
その半径と質量はどれぐらいにな
るか。同じく中心密度は
 を目安とせよ。
質量が中心密度によらない事を導け。
この事の意味する所を考察せよ。
を目安とせよ。
質量が中心密度によらない事を導け。
この事の意味する所を考察せよ。
Hansen, C. J. and Kawaler, S. D. 1994,
Stellar Interiors, (Springer-Verlag, New York).


Next: About this document ...
Up: 7 常微分方程式の数値解法:初期値問題
Previous: 1 Euler 法とRunge-Kutta 法
Jun Makino
平成15年5月29日
 を中心からの距離、
を中心からの距離、 をそこでの圧力、
をそこでの圧力、 を
その半径より内側に含まれる質量とすると、
を
その半径より内側に含まれる質量とすると、 を重力定数として、この力学平衡は、
次のように表す事が出来る。
を重力定数として、この力学平衡は、
次のように表す事が出来る。

 ,厚み
,厚み の球殻に含まれる質量
の球殻に含まれる質量 は、そこでの密度を
は、そこでの密度を とすると、
とすると、
 であるから、次の連続の式を得る。
であるから、次の連続の式を得る。

 と密度
と密度 は、ガスの成分、温度
は、ガスの成分、温度 によって決まっている。
即ち、
によって決まっている。
即ち、

 は、ガスに含まれる
は、ガスに含まれる 種の元素の質量比とする。
種の元素の質量比とする。
 は、エネルギー
の輸達の効率によって決められる。エネルギーの輸達の取りえる形態には、
輻射と対流と伝導があるが、通常の星の内部では伝導は効率が悪く、輻射か対流によ
っている。
は、エネルギー
の輸達の効率によって決められる。エネルギーの輸達の取りえる形態には、
輻射と対流と伝導があるが、通常の星の内部では伝導は効率が悪く、輻射か対流によ
っている。

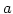 は輻射定数、
は輻射定数、 は光速、
は光速、 は吸収係数、
は吸収係数、 は半径
は半径 での光度、
での光度、 は断熱指数を表す。
は断熱指数を表す。

 、厚み
、厚み の球殻で発生するエネルギーを、
の球殻で発生するエネルギーを、
 と書くと、
と書くと、

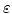 は、エネルギー発生率を表す。星のエネルギー源は核反応である。これは、
ガスの成分と状態によって決まる。
は、エネルギー発生率を表す。星のエネルギー源は核反応である。これは、
ガスの成分と状態によって決まる。

![\begin{displaymath}
\alpha \equiv \left[
{{(N+1)K}\over{4\pi G}} \rho_{\rm c}^{{{1}\over{N}}-1}
\right]^{1/2}
\end{displaymath}](img146.png)
![$\displaystyle \left[ {{(N+1)K}\over{4\pi G}}\right]^{1/2}
\rho_{\rm c}^{(1-N)/2N} \xi_1$](img174.png)




![\begin{displaymath}
M = -4\pi\left[{{(N+1)K}\over{4\pi G}}\right]^{3/2}
\rho_{\...
...3-N)/2N}
\left(\xi^2{{d\theta}\over{d\xi}}\right)_{\xi=\xi_1}
\end{displaymath}](img180.png)










