



Next: 10 レポート問題
Up: 9 常微分方程式の数値解法:固有値問題
Previous: 2 固有値問題としてのLane-Emden 方程式
Subsections
星自身の膨張収縮によって 光度変化をする一群の星(脈動変光星)がある。
HR 図上でセファイド不安定帯と呼ばれるところに位置する
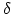 Cepheid型, RR Lyrae型,
Cepheid型, RR Lyrae型, 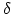 Sct型変光星や ミラ型変光星などの赤色
長周期変光星が古典的な脈動変光星として知られていた。
最近二十年ぐらいの間に、白色矮星や、A型特異星や、ほかならぬ太陽までが
非常に小さい振幅ながら脈動している事が判ってきた。
従って今では殆ど全ての星が大なり小なりの脈動をしていると考えられている。
これらの星の脈動は、それぞれの星の固有振動に他ならない。
固有値問題の例として、星の固有振動を解いてみよう。
Sct型変光星や ミラ型変光星などの赤色
長周期変光星が古典的な脈動変光星として知られていた。
最近二十年ぐらいの間に、白色矮星や、A型特異星や、ほかならぬ太陽までが
非常に小さい振幅ながら脈動している事が判ってきた。
従って今では殆ど全ての星が大なり小なりの脈動をしていると考えられている。
これらの星の脈動は、それぞれの星の固有振動に他ならない。
固有値問題の例として、星の固有振動を解いてみよう。
参考図書:坂下志郎・池内了 著「宇宙流体力学」(培風館)
- 連続の式
 |
(254) |
- 運動方程式
 |
(255) |
- エネルギーの式
 |
(256) |
- ポアソン方程式
 |
(257) |
- 輻射の式
 |
(258) |
平衡状態では、時間変動なし、運動なし、即ち
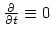 、
、
 とすると
とすると
- 運動方程式
 |
(259) |
- エネルギーの式
 |
(260) |
- ポアソン方程式
 |
(261) |
- 輻射の式
 |
(262) |
特に球対称として、
極座標
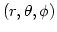 で記述すると
で記述すると
- 運動方程式
 |
(263) |
- 連続の式
 |
(264) |
- エネルギーの式
 |
(265) |
- 重力
 |
(266) |
- 輻射の式
 |
(267) |
これらは、星の平衡状態を記述する式に他ならない。
星の脈動の振幅は大きくないので、振動を平衡状態からのずれが小さいとして、平衡状
態からの線形摂動として取り扱う。
摂動には、二つの考え方がある。特定の場所を固定して見る立場と、特定の流体要素
に着目してみる立場で、前者は Euler 的摂動であり、後者は Lagrange 的摂動と呼ば
れる。
- Euler摂動
 |
(268) |
- Lagrange摂動
 |
(269) |
- 相互の関係
 |
(270) |
 |
(271) |
- Euler 微分 と Lagrange 微分
 |
(272) |
 |
(273) |
- 速度の Euler摂動 とLagrange摂動
 |
(274) |
従って、線形化した基礎方程式をEuler摂動について書くと
- 連続の式
 |
(275) |
- 運動方程式
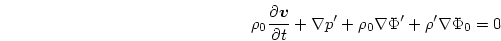 |
(276) |
- エネルギーの式
 |
(277) |
- ポアソン方程式
 |
(278) |
星の振動の時間尺度は
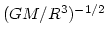 で、例えば太陽の場合、これは約1時間のオーダーである。
それに対し、熱の出入の時間尺度として
で、例えば太陽の場合、これは約1時間のオーダーである。
それに対し、熱の出入の時間尺度として
 を考えると、これは
星の表面近くを除けば振動の時間尺度に比べ桁違いに長い。そこで振動は断熱として
扱って良い。
そこでエネルギーの式は
を考えると、これは
星の表面近くを除けば振動の時間尺度に比べ桁違いに長い。そこで振動は断熱として
扱って良い。
そこでエネルギーの式は
 |
(279) |
となる。ここに 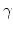 は断熱指数。
は断熱指数。
また重力の摂動も無視できるぐらいに小さい場合が殆どである。これは、星の固有振
動の多くは、密度の小さい外層で大きく揺れているので、重力に対する効果が小さい
ためである。
そこで、重力の摂動も無視することにする。
すると、
基礎方程式は
- 連続の式
 |
(280) |
- 運動方程式
 |
(281) |
- エネルギーの式
 |
(282) |
振動が球対称を保ったまま行なわれる場合、特に動径振動と称する。
前の節で述べてきた解析では、幾つかの近似を行って最後の微分方程式を簡単化した
が、動径振動を扱う場合には、厳密な式のままでも、簡単な式になるので、ここでは、
以下動径振動を考えよう。
Lagrange摂動で考えると簡単である。変位を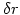 とすると、
連続の式(9.34)は、
とすると、
連続の式(9.34)は、
![\begin{displaymath}
{{d}\over{dt}}
\left({{\delta\rho}\over{\rho}}\right)+{{1}\o...
...}}{{d}\over{dr}}
\left[r^2{{(d\delta r)}\over{dt}} \right] = 0
\end{displaymath}](img704.png) |
(283) |
となる。
また、
運動方程式(9.35)は、
となる。
ここで、全ての摂動量の時間依存性を
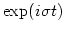 に比例するものとすると、
結局、連続の式、運動方程式、断熱の式は、
に比例するものとすると、
結局、連続の式、運動方程式、断熱の式は、
 |
(285) |
 |
(286) |
 |
(287) |
となる。ここで、相対変位
 |
(288) |
を定義し、これを使って表すと、連続の式は
 |
(289) |
となる。これを断熱の式に代入して
 |
(290) |
を得るから、これを運動方程式に代入すると、
![\begin{displaymath}
-\sigma^2r\xi = 4g\xi +{{1}\over{\rho}}{{d}\over{dr}}
\left[\gamma P\left(3\xi+r{{d\xi}\over{dr}}\right)\right]
\end{displaymath}](img715.png) |
(291) |
となる。
結局、整理すると、線形断熱動径振動の方程式は
![\begin{displaymath}
{{d}\over{dr}}\left[ r^4\gamma P {{d\xi}\over{dr}} \right]
+...
...{ \sigma^2\rho r^4 + r^3{{d}\over{dr}}[(3\gamma-4)P]\right\}=0
\end{displaymath}](img716.png) |
(292) |
となった。
境界条件は、中心で変位がゼロ、即ち、
 |
(293) |
と、表面が自由境界、即ち、
 |
(294) |
である。
上記方程式(9.46)は、
![\begin{displaymath}
{{d}\over{dr}}\left[\alpha (r) {{d\xi}\over{dr}}\right]
-\beta (r) \xi + \lambda \mu(r) \xi = 0
\end{displaymath}](img719.png) |
(295) |
の形であるから、Sturm-Liouville型の方程式である。
係数は
 |
(296) |
![\begin{displaymath}
\beta (r) = -r^3 {{d}\over{dr}}[(3\gamma - 4) P]
\end{displaymath}](img721.png) |
(297) |
 |
(298) |
に対応し、固有値は
 |
(299) |
である。これは固有振動数に他ならない。
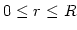 で、
で、
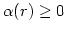 且つ
且つ
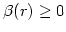 を満たしている。
Sturm-Liouville型の方程式の特性から、直ちに、
固有値
を満たしている。
Sturm-Liouville型の方程式の特性から、直ちに、
固有値 は実数の離散固有値であり、下限がある。
即ち、
は実数の離散固有値であり、下限がある。
即ち、
 |
(300) |
であり、対応する固有関数
 ,
, ,
,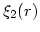 ,
, は節を
は節を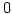 ,
,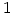 ,
, ,...
を持ち、固有関数
,...
を持ち、固有関数 の節は
の節は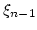 の節の間に各1ずつ位置する。
また、固有関数は、
の節の間に各1ずつ位置する。
また、固有関数は、
 |
(301) |
と正規直交系をなし、また、完全系をなす。
特別な場合として、密度一様な星を考えよう。平衡状態は、
 |
(302) |
 |
(303) |
 |
(304) |
である。無次元量
 |
(305) |
 |
(306) |
 |
(307) |
を導入すると、
 |
(308) |
であり、方程式(9.46)は、
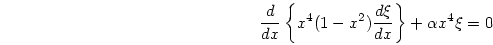 |
(309) |
となる。但し、ここに
 |
(310) |
である。
この場合の基本モードは、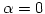 の場合である。これは、
の場合である。これは、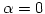 ならば、
解は
ならば、
解は
 となること明らかであろう。
これは、星全体がhomologousな振動をすることを意味している。固有値
となること明らかであろう。
これは、星全体がhomologousな振動をすることを意味している。固有値
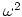 は
は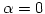 より、
より、
 |
(311) |
であるから、
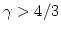 なら
なら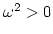 で
系は安定であり、逆に
で
系は安定であり、逆に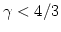 ならば、
ならば、 で、系は動的に不安定となる。
で、系は動的に不安定となる。
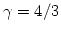 のとき、系は中立である。
のとき、系は中立である。
陪振動を求めよう。
 |
(312) |
として、(9.63)式に代入してみると、
 |
(313) |
 |
(314) |
を得る。対応する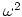 は、
は、
 |
(315) |
である。熱力学から、常に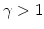 であるから、常に
であるから、常に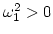 である。
以後同様にして高次の陪振動を求めて行く事が出来る。
である。
以後同様にして高次の陪振動を求めて行く事が出来る。
一般の星の場合でも、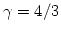 のときは、
のときは、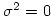 であり、
であり、
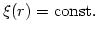 となる事は、(9.46)式から見て取れよう。
ただし、それ以外の場合は、数値的に解く必要がある。
となる事は、(9.46)式から見て取れよう。
ただし、それ以外の場合は、数値的に解く必要がある。
以下、
 とする。新たに無次元量
とする。新たに無次元量
 |
(316) |
と
 |
(317) |
を導入すると、(9.46)式は、
![\begin{displaymath}
x^2 {{d^2\xi}\over{dx^2}} + (4-V)x{{d\xi}\over{dx}}
+\left[ ...
...r{q}}\omega^2 - (3\gamma - 4)\right]
{{V}\over{\gamma}}\xi
=0
\end{displaymath}](img767.png) |
(318) |
となる。
一階二元連立微分方程式にするべく
 |
(319) |
 |
(320) |
を独立変数にすると、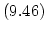 式は
式は
 |
(321) |
![\begin{displaymath}
{{dy_2}\over{dx}} =
-{{4-V}\over{x}}y_2
- \left[ {{x}\over...
...a^2 - {{3\gamma - 4}\over{x^2}} \right]
{{V}\over{\gamma}} y_1
\end{displaymath}](img772.png) |
(322) |
と表す事が出来る。
方程式は、星の中心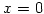 と表面
と表面 が特異点となっている。
そこで、解を求めるには、これらの近傍でLaurent展開をしてやらなければならない。
ポリトロープの場合、
が特異点となっている。
そこで、解を求めるには、これらの近傍でLaurent展開をしてやらなければならない。
ポリトロープの場合、
 |
(323) |
であり、中心近傍では
 |
(324) |
 |
(325) |
だから
![\begin{displaymath}
V \sim (N+1) \left[ {{x^2}\over{3}} + {{x^4}\over{18}} + ... \right]
\end{displaymath}](img776.png) |
(326) |
となる。 また、
 |
(327) |
に注意すると
 |
(328) |
である。そこで、中心近傍で、
![\begin{displaymath}
\xi \sim \xi_{\rm c}[1+ ax^n]
\end{displaymath}](img779.png) |
(329) |
とすると、(9.76)式の左辺は
 |
(330) |
だから、
 |
(331) |
であり、一方右辺は
![\begin{displaymath}
{\rm RHS} \sim
-\xi_{\rm c}\left[ 4- (N+1){{x^2}\over{3}}\ri...
...3\gamma -4)\right]
{{1}\over{\gamma}} {{N+1}\over{3}} (1+ax^n)
\end{displaymath}](img782.png) |
(332) |
である。両辺の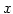 の次数を見ると、最低次は
の次数を見ると、最低次は の項であり、よって、
の項であり、よって、
![\begin{displaymath}
an(n-1)x^{n-2} \sim -[({\bar\rho}/\rho_{\rm c})\omega^2 -(3\gamma - 4)]
{{N+1}\over{\gamma}} x^0 - 4anx^{n-2}
\end{displaymath}](img784.png) |
(333) |
を得る。これより、
 |
(334) |
![\begin{displaymath}
10 a = -[{\bar\rho}/\rho_{\rm c} \omega^2 - (3\gamma - 4)]{{N+1}\over{3\gamma}}
\end{displaymath}](img786.png) |
(335) |
であるから、結局、解は
![\begin{displaymath}
y_1 \sim \xi_{\rm c}
\left\{1+{{1}\over{10}}[{\bar\rho}/\rho_{\rm c}\omega^2-(3\gamma -4)]
{{N+1}\over{3\gamma}}x^2\right\}
\end{displaymath}](img787.png) |
(336) |
![\begin{displaymath}
y_2 \sim \xi_{\rm c}
\left\{-{{1}\over{5}}[{\bar\rho}/\rho_{\rm c}\omega^2-(3\gamma -4)]
{{N+1}\over{3\gamma}}x\right\}
\end{displaymath}](img788.png) |
(337) |
となる。
ここで は未知であることに注意しておこう。
は未知であることに注意しておこう。
表面近傍の振舞を考えよう。
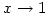 で
で
 |
(338) |
だから、解が正則であるためには、
(9.76)式の右辺で の項が釣り合う必要がある。そこで、
の項が釣り合う必要がある。そこで、
![\begin{displaymath}
{{V}\over{x}}y_2 - \left[{{x}\over{q}}\omega^2 - {{3\gamma -4}\over{x^2}}\right]
{{V}\over{\gamma}}y_1 \sim 0
\end{displaymath}](img793.png) |
(339) |
であり、よって、
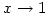 、
、
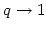 で
で
![\begin{displaymath}
y_2 \sim [\omega^2 - (3\gamma - 4)]{{1}\over{\gamma}}y_1
\end{displaymath}](img795.png) |
(340) |
を得る。これより、表面近傍での解は、表面で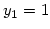 と規格化すると、
と規格化すると、
![\begin{displaymath}
y_1 \sim 1- [\omega^2 - (3\gamma - 4)]{{1}\over{\gamma}}(1-x)
\end{displaymath}](img797.png) |
(341) |
![\begin{displaymath}
y_2 \sim [\omega^2 - (3\gamma - 4)]{{1}\over{\gamma}}
\end{displaymath}](img798.png) |
(342) |
となる。
ここで、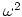 は未知である事に注意しておこう。
は未知である事に注意しておこう。
結局、中心近傍では が、表面近傍では
が、表面近傍では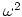 が未知のまま残った。
そこで、中心及び表面から、方程式を積分して行き、あるfitting point
が未知のまま残った。
そこで、中心及び表面から、方程式を積分して行き、あるfitting point
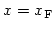 で、
で、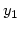 ,
,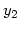 が共に一致すれば良い。内側の解、外側の解を表すた
めに、添字
が共に一致すれば良い。内側の解、外側の解を表すた
めに、添字 と
と をつけて表記すると、
をつけて表記すると、
 |
(343) |
を満たす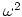 を探せば良い。
を探せば良い。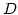 は
は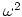 の関数であるから、
何点かの
の関数であるから、
何点かの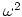 に対して、
に対して、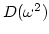 をプロットし、
をプロットし、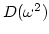 のゼロ点
を求めれば良い。それらのゼロ点が固有振動数である。
一旦固有振動数
のゼロ点
を求めれば良い。それらのゼロ点が固有振動数である。
一旦固有振動数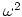 が求まったら、固有関数は直ちに求める事が出来よう。
が求まったら、固有関数は直ちに求める事が出来よう。
固有関数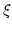 は表面で大きく、中心で小さい。また、密度の中心集中度が高い程、即
ち、
は表面で大きく、中心で小さい。また、密度の中心集中度が高い程、即
ち、
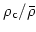 が大きい程、
が大きい程、
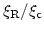 が大きい。
次元のある固有振動数
が大きい。
次元のある固有振動数 は
は
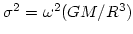 だから、これは平均
密度
だから、これは平均
密度 に比例する。従って、振動の周期は、平均密度の平方根に反比例す
る。
或いは、別の言い方をすると、モードが同じなら、異なる星について、
振動の周期
に比例する。従って、振動の周期は、平均密度の平方根に反比例す
る。
或いは、別の言い方をすると、モードが同じなら、異なる星について、
振動の周期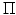 と平均密度の積は、ほぼ同一の値という事になる。例えば、
と平均密度の積は、ほぼ同一の値という事になる。例えば、
 に対して、
に対して、
 |
(344) |
である。
ポリトロープ星のモデルを使って、
波動方程式(9.46)
を数値的に解き、その固有値、固有関数を求めよ。
参考図書:
Kippenhahn, R. and Weigert, A. 1990, Stellar Structure and Evolution,
(Springer-Verlag, New York).
Hansen, C. J. and Kawaler, S. D. 1994, Steelar Interiors,
(Springer-Verlag, New York).
Table 9.1:
ポリトロープ星の固有振動(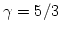 の場合)
の場合)
 |
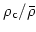 |
 |
 |
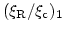 |
node of 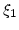 |
| 1.5 |
5.99 |
2.712 |
1.42 |
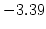 |
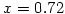 |
| 3.0 |
54.2 |
9.261 |
22.41 |
 |
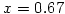 |
| 3.5 |
153. |
12.69 |
 |
|
|
| 4.0 |
622. |
15.38 |
 |
|
|
球対称なままの振動に限らない一般的な固有振動を記述する方程式を導出してみよう。
運動方程式 (9.35) の時間微分をとると
 |
(345) |
ここに
 |
(346) |
 |
(347) |
とする。
式(9.99)に rotation を二回作用させて
これより
 |
(349) |
を得る。
一方、式(9.99)の divergence をとると、
 |
(350) |
を得る。
式(9.103)と(9.104)より
 を消去すると、
を消去すると、
![\begin{displaymath}
{{\partial^4 \chi}\over{\partial t^4}}
-
{{\partial^2}\over...
...er{H_\rho}}\chi\right)\right] - c^2N^2\nabla_{\rm h}^2 \chi =0
\end{displaymath}](img831.png) |
(351) |
を得る。
ここで
 |
(352) |
で 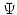 を定義すると、式(9.105)は
を定義すると、式(9.105)は
 |
(353) |
に帰する。ここで
 |
(354) |
これが星の振動を記述する波動方程式に他ならない。
波動関数の時間依存性を
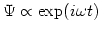 とする。また水平方向の空間依存性を
球面調和関数を使って
とする。また水平方向の空間依存性を
球面調和関数を使って
 とすると、式(9.108) は
とすると、式(9.108) は
 |
(355) |
と帰す。
これは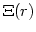 に関する二階の微分方程式で、
に関する二階の微分方程式で、
![\begin{displaymath}
{{d^2\Xi}\over{dr^2}} + {{1}\over{c^2\omega^2}}
[\omega^2-\omega_{+}^2(r)][\omega^2-\omega_{-}^2(r)]\Xi =0
\end{displaymath}](img840.png) |
(356) |
という形になっている。
(9.110)式は、中心と表面での適当な境界条件を科すことによって、固有値問題
に帰す。境界条件は、中心と表面で 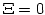 である。
である。
(9.110)式を、Schrödinger 方程式に対応させると、
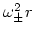 はポテンシャルの役割を果たしている事になる。
いままでに作った星のモデルを使って、関数
はポテンシャルの役割を果たしている事になる。
いままでに作った星のモデルを使って、関数
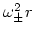 の具体的な形を数
値的に調べよ。
の具体的な形を数
値的に調べよ。
振動の復元力を考えよう。今考えている運動方程式では、重力とガス圧力しか入って
いない。ガス圧力は、星が収縮しようとすると圧力が高くなって反発させる。これは
振動としては音波に相当する。一方重力は、星のある水平面上でデコボコした波を考
えると判るように、重力面から出っ張った部分とへっこんだ部分を引き戻そうとして
振動になる。これが重力波である。
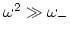 の場合、波動方程式(9.110)は、
の場合、波動方程式(9.110)は、
![\begin{displaymath}
{{d^2\Xi}\over{dr^2}} + {{1}\over{c^2}}
\left[\omega^2-{{l(l+1)c^2}\over{r^2}} - \omega_c^2\right]\Xi =0
\end{displaymath}](img844.png) |
(357) |
という形に帰する。ここで密度一定の星の場合 (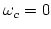 ) を考えると
判るように、これが音波モードを表わしている。実際、
) を考えると
判るように、これが音波モードを表わしている。実際、
 を水平方向の波数の二乗、
を水平方向の波数の二乗、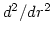 を鉛直方向の波数
の二乗
を鉛直方向の波数
の二乗  と考えれば、(9.111) は、音波の分散関係式
と考えれば、(9.111) は、音波の分散関係式
 |
(358) |
に帰する。
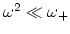 の場合、波動方程式(9.110)は、
の場合、波動方程式(9.110)は、
![\begin{displaymath}
{{d^2\Xi}\over{dr^2}} + {{l(l+1)N^2}\over{r^2}}
\left[{{1}\over{\omega^2}}-{{1}\over{N^2}}\right]\Xi =0
\end{displaymath}](img851.png) |
(359) |
という形に帰する。これは重力波モードを表わしている。実際、(9.113) は、
先程と同じ考えを使えば、重力波の分散関係式
 |
(360) |
に帰する。
適当な境界条件の下に、波動方程式(9.110)或いは(9.111)または
(9.113) は、振動数の二乗 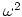 を固有値とする固有値問題になる。
Schrödinger 方程式に対応させて考えると、
を固有値とする固有値問題になる。
Schrödinger 方程式に対応させて考えると、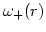 と
と  は、それぞれ音波モード、重力波モードの場合のポテンシャルに相当し、
は、それぞれ音波モード、重力波モードの場合のポテンシャルに相当し、
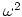 、
、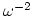 が固有値に相当する。
従って、星全体としての固有関数は
が固有値に相当する。
従って、星全体としての固有関数は
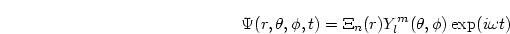 |
(361) |
と表わせ、これを規定する量子数には球面調和関数の指数  、
、 と
(9.110)或いは(9.111)または(9.113)の解
と
(9.110)或いは(9.111)または(9.113)の解 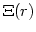 の節の数
の節の数  の3つがある。固有値
の3つがある。固有値 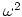 は3つの量子数のうち
は3つの量子数のうち  と
と には依るが、
には依るが、
 には依存せず、
には依存せず、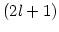 -重に縮退している。これは、方位量子数
-重に縮退している。これは、方位量子数  は特定の
方向を決めてこそ意味がある量であるのに、球対称の星では、特別の方向というもの
がないからである。そこで、自転の影響を考慮したりすると、この縮退は解ける。
この事情は Zeeman効果と同じである。
は特定の
方向を決めてこそ意味がある量であるのに、球対称の星では、特別の方向というもの
がないからである。そこで、自転の影響を考慮したりすると、この縮退は解ける。
この事情は Zeeman効果と同じである。
高調波モード  の場合を考える。波動方程式(9.111)及び
(9.113)について、量子数
の場合を考える。波動方程式(9.111)及び
(9.113)について、量子数 に関する量子化条件を考察せよ。
に関する量子化条件を考察せよ。
いままでに作った星のモデルを使って、
波動方程式(9.111)及び
(9.113)を の場合について、それぞれ
の場合について、それぞれ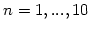 まで
数値的に解き、その固有値、固有関数を求めよ。
上で考えた量子化条件はどれぐらい良く満たされているか検討せよ。
まで
数値的に解き、その固有値、固有関数を求めよ。
上で考えた量子化条件はどれぐらい良く満たされているか検討せよ。




Next: 10 レポート問題
Up: 9 常微分方程式の数値解法:固有値問題
Previous: 2 固有値問題としてのLane-Emden 方程式
Jun Makino
平成15年4月17日
![]() Cepheid型, RR Lyrae型,
Cepheid型, RR Lyrae型, ![]() Sct型変光星や ミラ型変光星などの赤色
長周期変光星が古典的な脈動変光星として知られていた。
最近二十年ぐらいの間に、白色矮星や、A型特異星や、ほかならぬ太陽までが
非常に小さい振幅ながら脈動している事が判ってきた。
従って今では殆ど全ての星が大なり小なりの脈動をしていると考えられている。
これらの星の脈動は、それぞれの星の固有振動に他ならない。
固有値問題の例として、星の固有振動を解いてみよう。
Sct型変光星や ミラ型変光星などの赤色
長周期変光星が古典的な脈動変光星として知られていた。
最近二十年ぐらいの間に、白色矮星や、A型特異星や、ほかならぬ太陽までが
非常に小さい振幅ながら脈動している事が判ってきた。
従って今では殆ど全ての星が大なり小なりの脈動をしていると考えられている。
これらの星の脈動は、それぞれの星の固有振動に他ならない。
固有値問題の例として、星の固有振動を解いてみよう。
![]() 、
、
![]() とすると
とすると
![]() で記述すると
で記述すると
![]() で、例えば太陽の場合、これは約1時間のオーダーである。
それに対し、熱の出入の時間尺度として
で、例えば太陽の場合、これは約1時間のオーダーである。
それに対し、熱の出入の時間尺度として
![]() を考えると、これは
星の表面近くを除けば振動の時間尺度に比べ桁違いに長い。そこで振動は断熱として
扱って良い。
そこでエネルギーの式は
を考えると、これは
星の表面近くを除けば振動の時間尺度に比べ桁違いに長い。そこで振動は断熱として
扱って良い。
そこでエネルギーの式は
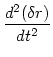
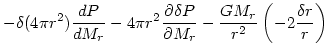

![]() とする。新たに無次元量
とする。新たに無次元量
![]() と表面
と表面![]() が特異点となっている。
そこで、解を求めるには、これらの近傍でLaurent展開をしてやらなければならない。
ポリトロープの場合、
が特異点となっている。
そこで、解を求めるには、これらの近傍でLaurent展開をしてやらなければならない。
ポリトロープの場合、
![]() で
で
![]() が、表面近傍では
が、表面近傍では![]() が未知のまま残った。
そこで、中心及び表面から、方程式を積分して行き、あるfitting point
が未知のまま残った。
そこで、中心及び表面から、方程式を積分して行き、あるfitting point
![]() で、
で、![]() ,
,![]() が共に一致すれば良い。内側の解、外側の解を表すた
めに、添字
が共に一致すれば良い。内側の解、外側の解を表すた
めに、添字![]() と
と![]() をつけて表記すると、
をつけて表記すると、
![]() は表面で大きく、中心で小さい。また、密度の中心集中度が高い程、即
ち、
は表面で大きく、中心で小さい。また、密度の中心集中度が高い程、即
ち、
![]() が大きい程、
が大きい程、
![]() が大きい。
次元のある固有振動数
が大きい。
次元のある固有振動数![]() は
は
![]() だから、これは平均
密度
だから、これは平均
密度![]() に比例する。従って、振動の周期は、平均密度の平方根に反比例す
る。
或いは、別の言い方をすると、モードが同じなら、異なる星について、
振動の周期
に比例する。従って、振動の周期は、平均密度の平方根に反比例す
る。
或いは、別の言い方をすると、モードが同じなら、異なる星について、
振動の周期![]() と平均密度の積は、ほぼ同一の値という事になる。例えば、
と平均密度の積は、ほぼ同一の値という事になる。例えば、
![]() に対して、
に対して、

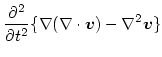

![]() とする。また水平方向の空間依存性を
球面調和関数を使って
とする。また水平方向の空間依存性を
球面調和関数を使って
![]() とすると、式(9.108) は
とすると、式(9.108) は
![]() の場合、波動方程式(9.110)は、
の場合、波動方程式(9.110)は、
![]() の場合、波動方程式(9.110)は、
の場合、波動方程式(9.110)は、
![]() を固有値とする固有値問題になる。
Schrödinger 方程式に対応させて考えると、
を固有値とする固有値問題になる。
Schrödinger 方程式に対応させて考えると、![]() と
と ![]() は、それぞれ音波モード、重力波モードの場合のポテンシャルに相当し、
は、それぞれ音波モード、重力波モードの場合のポテンシャルに相当し、
![]() 、
、![]() が固有値に相当する。
従って、星全体としての固有関数は
が固有値に相当する。
従って、星全体としての固有関数は