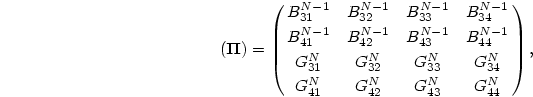Next: 9 常微分方程式の数値解法:固有値問題
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 3 現実的な恒星内部構造モデル
Subsections
星の内部構造を解く問題は、非線形の境界値問題であることを既に述べた。
主系列近傍の恒星の内部構造は、フィッティング法で解けた。
1960年代に恒星進化の理論は、主系列から赤色巨星への進化を追うようになったが、
赤色巨星になると、表面での境界値に対する依存性が鈍くなって、
フィッティング法では上手く解くことが出来なくなっていた。
こういった状況をブレークしたのは、カリフォルニア大学の
Henyeyであった。彼は、一種のrelaxation methodで代数方程式を解くことに
成功したのである
![[*]](footnote.png) 。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
![[*]](footnote.png) 。
。
問題とする微分方程式を
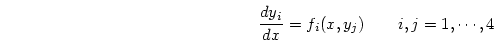 |
(192) |
とする。
独立変数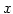 の領域を
の領域を メッシュに切って、微分方程式を差分方程式に書き換え、
これを数値的に解くことを考える。元の微分方程式を4階の微分方程式だとすると、
計
メッシュに切って、微分方程式を差分方程式に書き換え、
これを数値的に解くことを考える。元の微分方程式を4階の微分方程式だとすると、
計 本の差分方程式となる。これらは4つの変数
本の差分方程式となる。これらは4つの変数
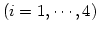 の
の
 個のメッシュそれぞれでの値、合計
個のメッシュそれぞれでの値、合計
 個の未知数、
個の未知数、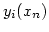 、の代数方程式と見なすことができる。
未知数の数と方程式の数が合わない?
このままでは、その通り。しかし、境界条件があることをお忘れなく。
内側の境界に境界条件が2本、外側の境界にも2本、合計4本の境界条件
の式があるので、方程式の数は合計
、の代数方程式と見なすことができる。
未知数の数と方程式の数が合わない?
このままでは、その通り。しかし、境界条件があることをお忘れなく。
内側の境界に境界条件が2本、外側の境界にも2本、合計4本の境界条件
の式があるので、方程式の数は合計 本になって、未知数の数と同じになり、
代数方程式は原理的に解けるのである。
ただ、これは「原理的に」である。
この方程式が非線形であれば、そのまま解くのが容易でないのは明らかであり、
線形であったとしても、
実際に数値的に解けるかどうかは、
本になって、未知数の数と同じになり、
代数方程式は原理的に解けるのである。
ただ、これは「原理的に」である。
この方程式が非線形であれば、そのまま解くのが容易でないのは明らかであり、
線形であったとしても、
実際に数値的に解けるかどうかは、
 による。実際的には、
による。実際的には、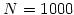 とすると、
とすると、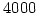 元の代数方程式
元の代数方程式
 |
(193) |
を解かねばならないことになり、これを直接、
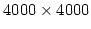 の行列
の行列
 の逆行列を計算して
の逆行列を計算して
 |
(194) |
とするのは、実際的ではない。
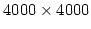 もの大行列の逆行列
を求めるのが困難だからである。
もの大行列の逆行列
を求めるのが困難だからである。
従属変数 の
の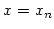 での値であることを表わすのに、上付き添え字
での値であることを表わすのに、上付き添え字 をつけて
をつけて
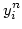 で表わすことにする:
で表わすことにする:
 |
(195) |
微分を差分に置き換えると、(8.105)式は
![\begin{displaymath}
{y^{n+1}_i-y^n_i\over\Delta x}
={1\over 2}[f_i(y_j^{n+1})+f_i(y_j^n)];
\quad i,j=1,\cdots,4;\quad n=1,2,\cdots,N-1
\end{displaymath}](img565.png) |
(196) |
となる。
但し、
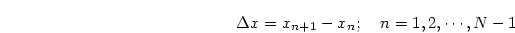 |
(197) |
である。
中心と表面での境界条件を、それぞれ、
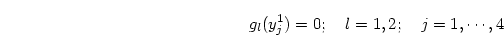 |
(198) |
と
 |
(199) |
としよう。
このままでは、方程式系は非線形である。推定値からのずれを取り扱うことにして、
問題を線形化しよう。
即ち、真の解 についての推定値を
についての推定値を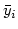 として、
真の値からのずれを
として、
真の値からのずれを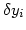 とする:
とする:
 |
(200) |
(8.113)式を
(8.109), (8.111), 及び(8.112)式に代入して、
 の2次以上の項を無視すると、
次の
の2次以上の項を無視すると、
次の 本の式を得る:
本の式を得る:
![\begin{displaymath}
\bar y_i^{n+1} +\delta y_i^{n+1} - \bar y_i^n - \delta y_i^n...
...n})}\over{\partial \bar y_j^{n}}}
\right];
\quad i=1,\cdots,4,
\end{displaymath}](img573.png) |
(201) |
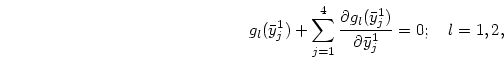 |
(202) |
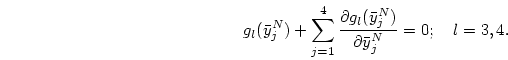 |
(203) |
整理すると、
 |
(204) |
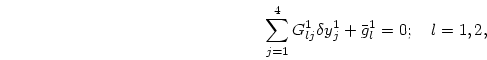 |
(205) |
それに
 |
(206) |
但し、ここに
 |
(207) |
 |
(208) |
![\begin{displaymath}
\bar d^n_i
=-(\bar y_i^{n+1}-\bar y_i^n)+{{\Delta x}\over{2}}[\bar f^{n+1}_i
+\bar f^n_i]
\end{displaymath}](img581.png) |
(209) |
であり、
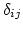 は Kroneckerのデルタを表す。
また、
は Kroneckerのデルタを表す。
また、
 |
(210) |
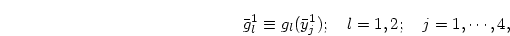 |
(211) |
 |
(212) |
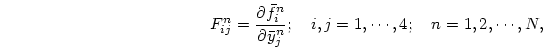 |
(213) |
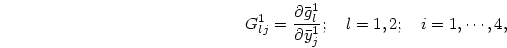 |
(214) |
 |
(215) |
で定義する。
方程式(8.117)-(8.119)は、 個の未知変数
個の未知変数 に関する
線形方程式である。
一見したところ、この方程式系は大行列を要し、解くことが出来ないと思えるかも知
れない。しかし、係数行列の要素の多くはゼロである。実際、
に関する
線形方程式である。
一見したところ、この方程式系は大行列を要し、解くことが出来ないと思えるかも知
れない。しかし、係数行列の要素の多くはゼロである。実際、
 、
、
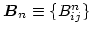 、
、
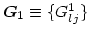 、
、
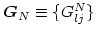 、
、
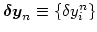 等と記して、方程式(8.117)-(8.119)を行列で表すと、
等と記して、方程式(8.117)-(8.119)を行列で表すと、
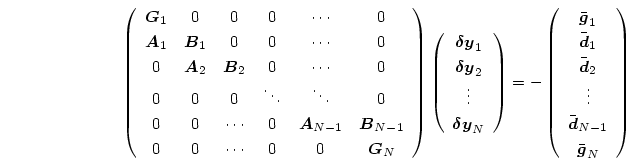 |
(216) |
になり、左辺の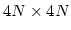 の係数行列の対角帯以外はゼロである。
Henyey法は、この特質を有効に利用するのである。
の係数行列の対角帯以外はゼロである。
Henyey法は、この特質を有効に利用するのである。
まず、2本の中心での
境界条件の式(8.118)と、最初の差分方程式(8.117)のうちから2本
( , 2)をセットにして考える。この4本の式は次の様に表される:
, 2)をセットにして考える。この4本の式は次の様に表される:
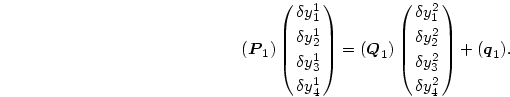 |
(217) |
ここに
 |
(218) |
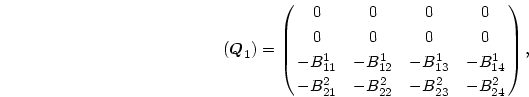 |
(219) |
 |
(220) |
である。
この4本の方程式は、8個の未知変数 、
、

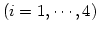 を含むから、
を含むから、
 個の変数は、残り4個の変数の線形従属として表すことが出来る。即ち、
個の変数は、残り4個の変数の線形従属として表すことが出来る。即ち、
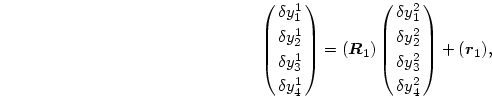 |
(221) |
但し、ここに
 |
(222) |
 |
(223) |
であり、
 は
は
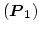 の逆行列を表す。
(8.134)式は、一旦
の逆行列を表す。
(8.134)式は、一旦
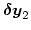 が求まれ
ば、
が求まれ
ば、
 が求められる
ことを意味している。
が求められる
ことを意味している。
次に、 の(8.117)式の残りの2本
の(8.117)式の残りの2本 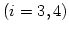 と、
と、 の(8.117)式の最初の2本
の(8.117)式の最初の2本  のセットを考える。
このセットは
のセットを考える。
このセットは
 |
(224) |
と表される。但し、ここで
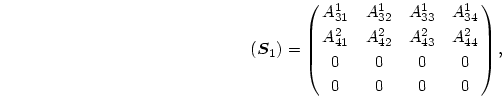 |
(225) |
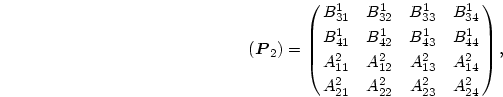 |
(226) |
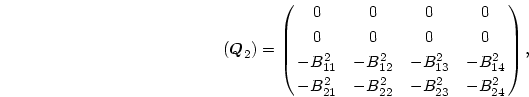 |
(227) |
それに
 |
(228) |
である。
(8.134)式を(8.137)式に代入して、
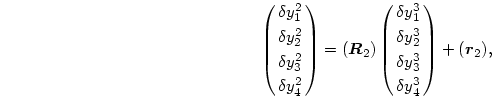 |
(229) |
を得る。但し、ここで、行列
 と
と
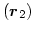 は
は
![\begin{displaymath}
(\mbox{\boldmath$R$}_2)
=\left[(\mbox{\boldmath$S$}_1)(\mb...
...
+(\mbox{\boldmath$P$}_2)\right]^{-1}(\mbox{\boldmath$Q$}_2),
\end{displaymath}](img623.png) |
(230) |
![\begin{displaymath}
(\mbox{\boldmath$r$}_2)
=\left[(\mbox{\boldmath$S$}_1)(\mb...
...q$}_2)-(\mbox{\boldmath$S$}_1)
(\mbox{\boldmath$r$}_1)\right]
\end{displaymath}](img624.png) |
(231) |
で定義する。
(8.142)式は
 |
(232) |
と一般化した漸化式に書くことが出来る。但し、
![\begin{displaymath}
(\mbox{\boldmath$R$}_n)
=\left[(\mbox{\boldmath$S$}_{n-1})...
...
+(\mbox{\boldmath$P$}_n)\right]^{-1}(\mbox{\boldmath$Q$}_n),
\end{displaymath}](img626.png) |
(233) |
![\begin{displaymath}
(\mbox{\boldmath$r$}_n)
=\left[(\mbox{\boldmath$S$}_{n-1})...
...(\mbox{\boldmath$S$}_{n-1})(\mbox{\boldmath$r$}_{n-1})\right],
\end{displaymath}](img627.png) |
(234) |
であり、
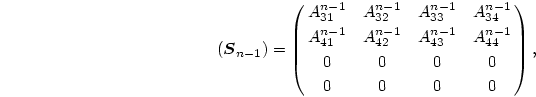 |
(235) |
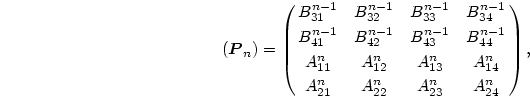 |
(236) |
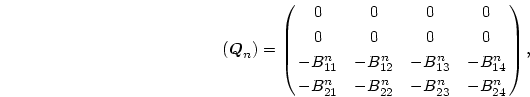 |
(237) |
それに
 |
(238) |
である。
(8.145)式は、一旦
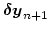 が求まれば、
が求まれば、
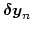 が求められる
ことを意味している。問題をいつまでも先送りしているだけの様に見えるかもしれな
いが、そうではない。
が求められる
ことを意味している。問題をいつまでも先送りしているだけの様に見えるかもしれな
いが、そうではない。
一番外側のメッシュ点 では、
では、
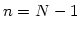 での(8.117)式の残りの2本の式と
表面での2本の境界条件
(8.112)式とで
での(8.117)式の残りの2本の式と
表面での2本の境界条件
(8.112)式とで
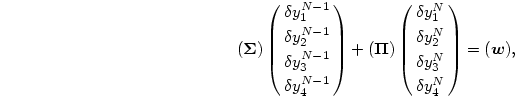 |
(239) |
を得る。但し、ここで、
 |
(240) |
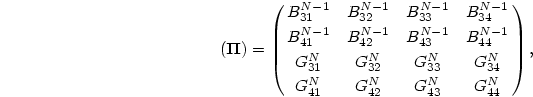 |
(241) |
それに
 |
(242) |
である。
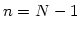 の(8.145)式を(8.152)式に代入すれば、
の(8.145)式を(8.152)式に代入すれば、
 次の正方行列
次の正方行列

![\begin{displaymath}
(\mbox{\boldmath$Z$})\equiv
\left[(\mbox{\boldmath$\Sigma$})(\mbox{\boldmath$R$}_{N-1})
+(\mbox{\boldmath$\Pi$})\right]
\end{displaymath}](img641.png) |
(243) |
と
列ベクトル
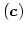
![\begin{displaymath}
(\mbox{\boldmath$c$})\equiv
[(\mbox{\boldmath$w$})-(\mbox{\boldmath$\Sigma$})
(\mbox{\boldmath$r$}_{N-1})]
\end{displaymath}](img643.png) |
(244) |
を使って、
 |
(245) |
となるが、
(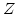 )の逆行列を
(8.158)式にあてがえば、
)の逆行列を
(8.158)式にあてがえば、
 |
(246) |
を得る。こうして、ここにきて、一番外側のメッシュ点での解
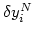
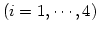 が求められるのである。一旦、
が求められるのである。一旦、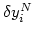 が決まれば、
これを
が決まれば、
これを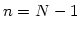 に対する(8.145)式に代入すれば、
に対する(8.145)式に代入すれば、
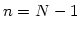 についての解
についての解  を得る。同様の操作を繰り返し、
解
を得る。同様の操作を繰り返し、
解  が順次得られる寸法だ。
が順次得られる寸法だ。
 が充分小さくなるまで補正を繰り返してや
れば、逐次解を得ることが出来る。
が充分小さくなるまで補正を繰り返してや
れば、逐次解を得ることが出来る。
こうして、非線形常微分方程式の境界値問題を、推定した解の近傍で線形化して、解
くことが出来ることが判ったと思う。線形化した点が、Henyey法の真髄ではない。
線形化して得た、方程式(8.129)を、左辺の大きい係数行列の逆行列を求め
るのが困難なところを、小行列に区分化して、解いていった点が本質なのである。
元の係数行列は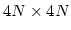 次であった。それに対して、Henyey法では
次であった。それに対して、Henyey法では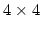 の区分行列を
の区分行列を 回取り扱うのである。行列の演算は、行列の次元の二乗に比例する
から、元の係数行列そのものの逆行列演算は
回取り扱うのである。行列の演算は、行列の次元の二乗に比例する
から、元の係数行列そのものの逆行列演算は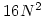 に比例するのに対し、Henyey法で
は、
に比例するのに対し、Henyey法で
は、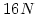 にしか比例しない。従って、
にしか比例しない。従って、 が大きくなるにつれて、Henyey法の優越性
が顕著となる。
が大きくなるにつれて、Henyey法の優越性
が顕著となる。




Next: 9 常微分方程式の数値解法:固有値問題
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 3 現実的な恒星内部構造モデル
Jun Makino
平成15年4月17日
![[*]](footnote.png) 。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
![[*]](footnote.png) 。
。
![[*]](footnote.png) 。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
。
この方法は、一般の2点境界値問題に適用出来る方法で、
天文学の社会では、Henyey法と呼ばれている。
以下に、このHenyey法を解説しよう
![[*]](footnote.png) 。
。
![]() の
の![]() での値であることを表わすのに、上付き添え字
での値であることを表わすのに、上付き添え字![]() をつけて
をつけて
![]() で表わすことにする:
で表わすことにする:
![\begin{displaymath}
\bar y_i^{n+1} +\delta y_i^{n+1} - \bar y_i^n - \delta y_i^n...
...n})}\over{\partial \bar y_j^{n}}}
\right];
\quad i=1,\cdots,4,
\end{displaymath}](img573.png)
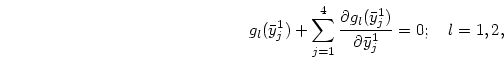
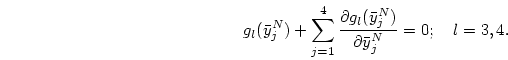



![]() の(8.117)式の残りの2本
の(8.117)式の残りの2本 ![]() と、
と、![]() の(8.117)式の最初の2本
の(8.117)式の最初の2本 ![]() のセットを考える。
このセットは
のセットを考える。
このセットは
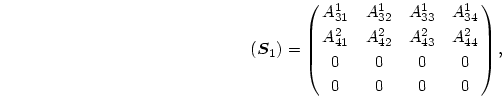
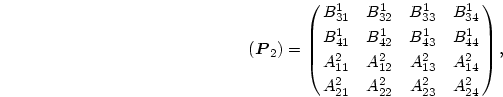
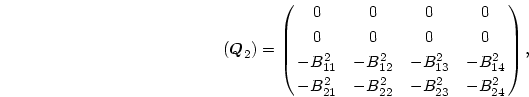

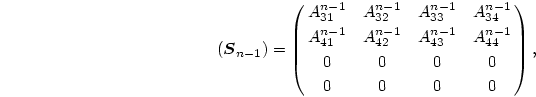
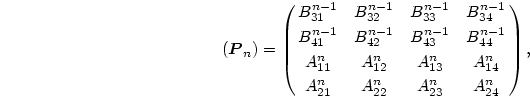
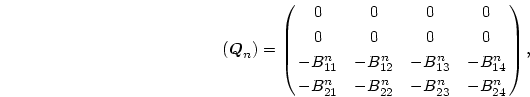

![]() では、
では、
![]() での(8.117)式の残りの2本の式と
表面での2本の境界条件
(8.112)式とで
での(8.117)式の残りの2本の式と
表面での2本の境界条件
(8.112)式とで