



Next: 2 ポリトロープガス球とLane-Emden方程式
Up: 7 常微分方程式の数値解法:初期値問題
Previous: 7 常微分方程式の数値解法:初期値問題
Subsections
簡単のために、一元の微分方程式の場合を考えよう:
 |
(28) |
 の周りでの Taylor展開を利用する事はすぐに思いつくだろう:
の周りでの Taylor展開を利用する事はすぐに思いつくだろう:
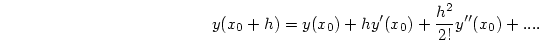 |
(29) |
ここで、
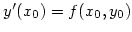 だから、
だから、 までは、Taylor展開で求める事が
出来る。即ち、
までは、Taylor展開で求める事が
出来る。即ち、
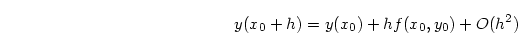 |
(30) |
誤差は
 |
(31) |
のオーダーである。この方法による計算は、Euler法と呼ばれる。
Figure 7.1:
Euler法による積分の概念図。
 |
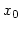 と
と  の間の、中間の
の間の、中間の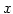 における導関数、
における導関数、 の関数値を何回か
計算し、それらの適当な平均を用いる事によって、高次の Taylor展開を達成しよう
というのが、Runge-Kutta 法である。
の関数値を何回か
計算し、それらの適当な平均を用いる事によって、高次の Taylor展開を達成しよう
というのが、Runge-Kutta 法である。
次の例で説明しよう。
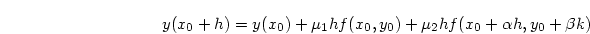 |
(32) |
と表す。
右辺第二項は、点 での傾き
での傾き
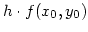 に
に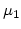 の
重みを掛けたものであり、第三項は、
の
重みを掛けたものであり、第三項は、
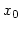 と
と  の間のある点
の間のある点
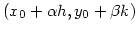 での傾き
での傾き
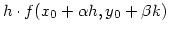 に
に の重みを掛けたものである。即ち、第二項と第三項とで、
の重みを掛けたものである。即ち、第二項と第三項とで、
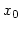 と
と  の間の、中間の
の間の、中間の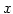 における導関数、
における導関数、 の関数値
の適当な平均を用いて、
の関数値
の適当な平均を用いて、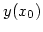 から
から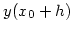 を求める事を考える。
ここで、
を求める事を考える。
ここで、
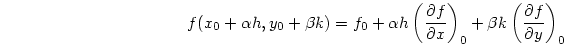 |
(33) |
だから、(7.6)式は、
となる。
この式と(7.3)式とを比べれば、
 |
(35) |
 |
(36) |
 |
(37) |
ならば、(7.9)式は、Taylor展開に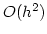 の精度まで一致する事が判る。
の精度まで一致する事が判る。
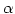 ,
,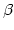 や重み
や重み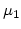 ,
, はユニークではない。
はユニークではない。
特に、
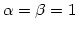 ,
,
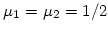 の時は、
の時は、
![\begin{displaymath}
y(x_0+h) = y(x_0) + {{1}\over{2}}[h f_0 + h f_0(x_0 + h,y_0 + h f_0)]
\end{displaymath}](img199.png) |
(38) |
で、これを改良Euler公式、或いは、Heun の二次公式と呼ぶ。
 ,
, ,
,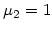 の場合は、
の場合は、
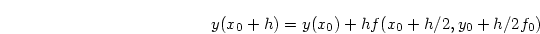 |
(39) |
で、これは修正Euler公式と呼ばれる。
改良Euler公式も修正Euler公式も、幾何学的に考えれば、意味は明らかであろう。
Figure 7.2:
修正Euler法による積分の概念図。
 |
ここでは証明は略すが、
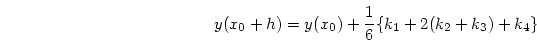 |
(40) |
但し、
 |
(41) |
 |
(42) |
 |
(43) |
 |
(44) |
とすると、
(7.14)式は、
Taylor展開の四次の精度までを持つ。通常、(7.14)式をRunge-Kuttaの公式と呼ぶ。
Runge-Kuttaの公式のサブルーチンプログラムの例を下に掲げる。このプログラムでは、
 元連立一次方程式で、
元連立一次方程式で、
 は与えられているとして、
は与えられているとして、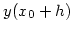 を計算する。
中間点での導関数を与えるプログラムは、別のサブルーチンで与えられているとして、
それをDERIVSと呼んでいる。この名前は仮の名前だから、引数として扱っている。
メインプログラムでは、external文を使って、導関数を与えるプログラムを指定
しておくだけで良い。
を計算する。
中間点での導関数を与えるプログラムは、別のサブルーチンで与えられているとして、
それをDERIVSと呼んでいる。この名前は仮の名前だから、引数として扱っている。
メインプログラムでは、external文を使って、導関数を与えるプログラムを指定
しておくだけで良い。
subroutine RK4(y,dydx,n,x,h,yout,DERIVS)
implicit NONE
real*8 y,dydx,yout,yt,dyt,dym,
& x,xh,h,hh,h6
integer nmax,n,i
parameter (nmax=2)
dimension y(n),dydx(n),yout(n),yt(nmax),dyt(nmax),dym(nmax)
hh=h*0.5
h6=h/6.
xh=x+hh
Do i=1,n
yt(i)=y(i)+hh*dydx(i)
End do
call DERIVS(xh,yt,dyt)
Do i=1,n
yt(i)=y(i)+hh*dyt(i)
End do
call DERIVS(xh,yt,dym)
Do i=1,n
yt(i)=y(i)+h*dym(i)
dym(i)=dyt(i)+dym(i)
End do
call DERIVS(x+h,yt,dyt)
Do i=1,n
yout(i)=y(i)+h6*(dydx(i)+dyt(i)+2.*dym(i))
End do
Return
End
Runge-Kutta法とEuler法と修正Euler法を使って、次の連立一階常微分方程式を解き、
誤差を評価せよ。
 |
(45) |
但し、初期値は
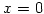 で
で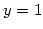 ,
,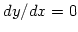 とし、
区間
とし、
区間 ![$x= [0, \pi/2]$](img215.png) について解け。
尚、先に挙げたサブルーチン RK4 の使用例として、
Runge-Kutta法でのサンプルプログラムを下に掲げる。
について解け。
尚、先に挙げたサブルーチン RK4 の使用例として、
Runge-Kutta法でのサンプルプログラムを下に掲げる。
program main
implicit NONE
real*8 y,dydx,x,h,yout,pi
integer i
parameter(i=2,h=0.001,pi=3.141593)
dimension y(i),dydx(i),yout(i)
external diff_eq
open(unit=1,file='RK_sample1.dat',status='new')
c initial value
x = 0.
y(1) = 1.
y(2) = 0.
c do loop
do while (x.le.pi/2.)
write(1,100) x,y(1),y(2)
call diff_eq(x,y,dydx)
call rk4(y,dydx,2,x,h,yout,diff_eq)
y(1) = yout(1)
y(2) = yout(2)
x = x + h
end do
100 format(11x,f6.3,1p2e12.4)
close(1)
stop
end
subroutine diff_eq(x,y,dydx)
implicit NONE
real*8 y,dydx,x,n
dimension y(2),dydx(2)
dydx(1)=y(2)
dydx(2)=-y(1)
return
end
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. 1992,
Numerical Recipes in FORTRAN 77 (Second Edition),
(Cambridge University Press, Cambridge).
http://cfatab.harvard.edu/nr/nronline.html




Next: 2 ポリトロープガス球とLane-Emden方程式
Up: 7 常微分方程式の数値解法:初期値問題
Previous: 7 常微分方程式の数値解法:初期値問題
Jun Makino
平成15年4月17日
![]() だから、
だから、![]() までは、Taylor展開で求める事が
出来る。即ち、
までは、Taylor展開で求める事が
出来る。即ち、
![]() ,
,
![]() の時は、
の時は、
![]() 元連立一次方程式で、
元連立一次方程式で、
![]() は与えられているとして、
は与えられているとして、![]() を計算する。
中間点での導関数を与えるプログラムは、別のサブルーチンで与えられているとして、
それをDERIVSと呼んでいる。この名前は仮の名前だから、引数として扱っている。
メインプログラムでは、external文を使って、導関数を与えるプログラムを指定
しておくだけで良い。
を計算する。
中間点での導関数を与えるプログラムは、別のサブルーチンで与えられているとして、
それをDERIVSと呼んでいる。この名前は仮の名前だから、引数として扱っている。
メインプログラムでは、external文を使って、導関数を与えるプログラムを指定
しておくだけで良い。