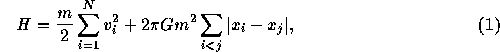
The Hamiltonian of the sheet model is given by
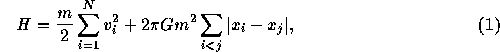
where 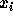 and
and 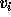 are the position and velocity of sheet i, m
is the mass of the sheets, N is the number of the sheets and G is
the gravitational constant. The crossing time is defined as
are the position and velocity of sheet i, m
is the mass of the sheets, N is the number of the sheets and G is
the gravitational constant. The crossing time is defined as

where M=mN is the total mass of the system. Following Tsuchiya
et al.[12] and others, we use
the system of units in which 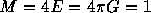 . In this system,
. In this system, 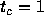 .
.
A unique nature of the one-dimensional gravitational system is that there exists the thermal equilibrium, unlike its counterpart in three dimensions. Rybicki [8] obtained the distribution function
where  is the specific binding energy defined as
is the specific binding energy defined as
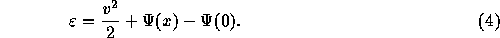
Here, 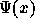 is the specific potential energy. This distribution
function satisfies the relation
is the specific potential energy. This distribution
function satisfies the relation
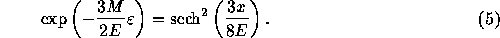
We performed the time integration of the system with N=16, 32, 64,
128 and 256. For all systems, the initial condition is a water-bag
with the aspect ratio 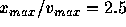 .
.
The important character of the sheet model is that one can calculate
the exact orbit of each sheet until two sheets cross each other. Thus,
we can integrate the evolution of the system precisely (except for the
round-off error). This may
sound like a great advantage, compared to the systems in higher
dimensions whose orbits can be calculated only numerically. Instead
of numerically integrating the orbit of each sheet, we can calculate
the exact orbit for any sheet, until it collides with the neighboring
sheet. Thus, by arranging the pairs using heap, we can handle each
collision in 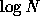 calculation cost.
calculation cost.
Note, however, that typically each sheet collides with all other
sheets in one crossing time. Thus, the calculation cost is 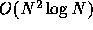 per crossing time. Our simulation with N=64 for
per crossing time. Our simulation with N=64 for 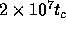 took 8 hours on a VT-Alpha workstation with DEC Alpha 21164A CPU
running at 533 MHz. For this run, the total energy of the system was
conserved better than
took 8 hours on a VT-Alpha workstation with DEC Alpha 21164A CPU
running at 533 MHz. For this run, the total energy of the system was
conserved better than 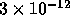 .
.