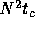 , where
, where 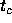 is the crossing time of the
system.
is the crossing time of the
system.
The one-dimensional self-gravitating many-body system was originally
discussed mainly as a simple toy model to understand the violent
relaxation, [4] because the thermal relaxation
timescale of its discrete realization, the sheet model, was believed
to be long. Until 1980s, it had been generally accepted that the
thermal relaxation time of the system of N equal-mass sheets is of
the order of 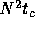 , where
, where 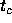 is the crossing time of the
system.
is the crossing time of the
system.
However, by means of numerical simulation Luwel et
al.[3] have demonstrated that the relaxation time is of
the order of 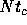 . Reidel and Miller [6,7]
reached a similar conclusion, though they reported the presence of
systems which apparently did not relax for much longer timescale.
. Reidel and Miller [6,7]
reached a similar conclusion, though they reported the presence of
systems which apparently did not relax for much longer timescale.
In a series of papers, Tsuchiya et al.
[10,11,12] have studied the thermal
relaxation process of one-dimensional self-gravitating systems in
detail, by means of the numerical integration over very long timescale
(some of their experiments covered 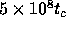 ). They claimed
that the thermal relaxation of the sheet model proceeds in a
highly complex manner. In the ``microscopic relaxation timescale'' of
). They claimed
that the thermal relaxation of the sheet model proceeds in a
highly complex manner. In the ``microscopic relaxation timescale'' of
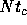 , each sheet forgets its initial condition, and the system is
well mixed. However, according to them, the system does not really
reach the thermal equilibrium in this timescale, and the distribution
function remains different from that of the isothermal state. They
called this state a quasiequilibrium
, each sheet forgets its initial condition, and the system is
well mixed. However, according to them, the system does not really
reach the thermal equilibrium in this timescale, and the distribution
function remains different from that of the isothermal state. They
called this state a quasiequilibrium
By pursuing the time integration for much longer timescale, Tsuchiya et al. [12] found that the system exhibits the transition from one quasiequilibrium to another, and they claimed that the thermal equilibrium is only realized by averaging over the timescale longer than the timescale of these transitions. Thus, they argued that there exists the timescale for ``macroscopic'' relaxation, which is much longer than the usual thermal relaxation (what they called ``microscopic relaxation'').
In this paper, we try to examine the nature of this ``macroscopic'' relaxation of the one-dimensional sheet model. In section 2, we describe the numerical model. In section 3, we present the result of the measurement of the relaxation time. It is shown that the relaxation time, defined as the timescale in which individual sheets change their energies, depends very strongly on the energy itself, and is very long for high energy sheets. This strong dependence of the relaxation timescale on the energy naturally explains the apparent ``transient'' phenomena observed by Tsuchiya et al.[12] Section 4 discusses the implication and relevance of our results.