
ここでいう可積分性とは、系の振舞いが十分な数の保存量によって制限されて いて、それらと時間の関数の形に解が書き下せるということである。例えば1 次元調和振動子

を考えてみると、この解というのはxと 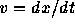 の空間では円上を等角速
度で運動することになる。従って、初期条件がわかれば任意の時刻での「解が
わかる」。数学的には、ハミルトン系(普通の、運動方程式が書けるような系。
ただし、摩擦とかがない理想的なもの)では、自由度の数の2倍マイナス1個だけ
保存量があれば可積分であるということになる。
の空間では円上を等角速
度で運動することになる。従って、初期条件がわかれば任意の時刻での「解が
わかる」。数学的には、ハミルトン系(普通の、運動方程式が書けるような系。
ただし、摩擦とかがない理想的なもの)では、自由度の数の2倍マイナス1個だけ
保存量があれば可積分であるということになる。
N自由度のハミルトン系の状態は 2N次元の空間のなかの1点として表現で き、系の時間発展はそのなかの軌道として表現できる。 大雑把にいうと、保存量が1つ増えれば解(軌道)の存在できる空間が1次元減 る。2N-1あると 1 次元に落ちるわけである。
自由度が増えたり、あるいは非線形の方程式になっても、もちろんこのような 解がある場合というものもある。例えば、太陽の回りの惑星の運動というの は、(惑星が1つだけなら)可積分である。これは、周期解があるということ からも想像がつくであろう。
しかし、惑星が2つになって、そのあいだの相互作用があると、これはもう可 積分ではない。この場合にも、相互作用の効果を近似的に付け加えていく摂動 法のようなものが使える場合もあるが、それでは済まないような場合も無数に ある。
たとえば、図に示すのは、3体問題の計算例である。これは1981年に でた論文からとった図である。こういったものは、周期解に近いと思ってなん とかできるものではないということはわかるであろう。
こういった、面倒な話というのは世の中にいっぱいあって、可積分とか、それ に近いとかいったことを前提にする方法では対応できないわけである。

さて、可積分でないといっても、「解がない」わけではない。上の図はまさに そういった解を示しているわけである。
この解を求めるのはどうやったのであろうか?もちろん、計算機で計算しても とめたわけである。しかし、計算してといわれても、実際にどんなプログラム で何を計算したのだろうか?また、この答えは「合っている」のだろうか?そ もそも計算機で求まった答があっているとか間違っているとかはどうやって判 断するのだろうか?
といったようなことを、この講義では考えていくことにしたい。