2 数値解の安定性

これから数値解の安定性というものを考える。もとの解が定常解を持てば、数 値解の安定性というのは要するにその定常解がやはり安定である、つまりそこ から少し離れたところから出発すると、必ずその定常解にいくということである。

極限周期軌道を持つ場合にも安定性の概念を拡張することができる。が、これ についてはあまり詳しくはここでは扱わない。とりあえず、もとの方程式が線 形で安定な定常解を持つ場合に、数値解の安定性とはどういうことかを考えて いこう。

2.1 陽的オイラー法の安定性

一変数線形常微分方程式

を、前進（陽的）オイラー法

で積分する場合を考えてみる。すぐにわかるように、

から、

となる。安定であるとは 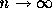で と なることであるから、その条件は

つまり

ということになる。

すこし考えてみるとすぐにわかるように、 の数値解は解とし てはむちゃくちゃなものであるが、まあ、それでも安定ではある。

さて、多変数の場合はどうなるかということを考えると、結局、線形の場合は 対角化してしまえば一変数の場合と全く同じで、各変数が安定であればいい。 ただし、少し違うのは、複素数の固有値が発生するということである。このため に、安定性条件が式(18)から簡単にならない。そこ で、通常、 とおいてこれがどういう範囲であれば安定 かという議論をする。

一変数（実固有値）の場合には、安定であるのはが開区間 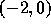にある場合である。複素数の固有値のときは、複素平面上で考えると、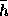が中心 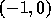、半径 1 の円の 内部で安定ということになる。なお、上のような、元の方程式に安定解がある 時に数値解がそこにいくという性質を、特に「絶対安定性」ということがあり、 の複素平面上で絶対安定である領域のことを絶対安定領域という。

前進オイラー法の絶対安定領域はあまり広くない。が、それが問題にならない ような場合も結構多いということがわかるであろう。普通は h は となるようにとる。この時は、不安定になるのは固有値の虚 部が実部に比べて大きい場合に限られる。

2.2 後退オイラー法の安定性

後退（陰的）オイラー法

で積分する場合を考えてみる。すぐにわかるように、

から、

となる。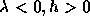なので 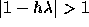であり、後退オイラー 法の絶対安定領域は左半平面全体であるということがわかる。言い替えれば、

後退オイラー法は数値不安定を起こすことはない。

これは、前進オイラー法に比べた後退オイラー法の目覚しい特徴である。

2.3 線形多段階法の安定性に関する一般論

一般に線形多段階法についてはオイラー法と同様な扱いができる。つまり、使 う公式を決めたら、それで一変数線形の方程式を解いて見る。すると、それが 一般に の形をとる。 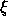は、安定性多項式と呼ばれる、要 するに 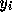を で置き換えてできる代数方程式の根である。このと き、絶対安定である条件は、すべての の絶対値が 1 より小さいとい うことになる。

例えば、前回の補外法のところで出てきた中点公式

を考えてみよう。安定性多項式は

となり、実解が2つある。すぐにわかるように、 ならば必 ず解の一つは絶対値が 1 より大きいので、中点公式には絶対安定領域がない、 言い替えればかならず不安定であるということがわかる。

これにたいし、アダムス法はちゃんと絶対安定領域を持つ。但し、次数が上が るにつれて小さくなるし、陽公式の安定領域は陰公式のそれよりもずっと狭い。

2.4 陽的ルンゲ・クッタ公式の安定性

ルンゲ・クッタ公式についても、線形多段階法の場合と同様に絶対安定領域を 求めることが出来る。陽的公式については、以下の面白い結果が知られている

• 4次までの公式（段数と次数が等しいもの）の絶対安定領域は、次数だ けで決まる。
• 4次まででは高次の公式のほうが安定領域が広い。

5次以上では、公式によって安定領域が違う。精度と安定領域のどちらを優先 するかでさまざまな公式が作られている。

2.5 陰的ルンゲ・クッタ公式の安定性

陰的ルンゲクッタについては、陽的公式よりもはるかに強い結果が得られてい る:陰的ガウス公式の安定領域は、左半平面全体である。また、Radau 公式、 Lobatto 公式についても同様である。

これは、陰的公式、とくに full-implicit な公式の重要な利点の一つである。

2.6 補外法の安定性

良くわかっていない。 h のとりかたを決めれば、ルンゲ・クッタの一種と みなせるので、そういう研究はある。具体例では、割と狭いという結果が得ら れているようである。