1 陰的ルンゲ・クッタ公式の続き

ええと、先週には、次はガウス型公式の話をするといったが、他との関係もあ るので数値積分の基礎的な話をもう少しやってからそっちにいこう。

1.1 数値積分に関する話の続き

ニュートン・コーツ型の公式の一般形についてはすでに説明したが、あれでは 具体的なことが良くわからないと思うので例によって次数が低いものを構成し てみる。

を区間 （これは、すでに適当に分割したあとの狭い区間である と思って欲しい）で数値的に積分するのに、例えば関数を1度だけ計算すると すれば、以下のようにいろいろなものが考えられる

これらは、それぞれ、その区間で関数の値が定数であると近似して、その定数 を積分したというふうに解釈できる。もちろん、中点以外の任意の点をとるこ とも考えられる。

計算精度という観点からは、中点をとることには非常に特別な性質がある。つ まり、この場合だけ局所誤差が になるのである。これは、テイラー 展開の1次の項が積分すると消えることから容易に示すことができる。という わけでこれには名前がついていて、中点公式という。

さて、それでは、2度計算していいとすればどうであろうか？普通に考えつく のは先週も書いた台形公式である。つまり、関数を

で近似して、それを積分して求まる

を積分の値として使うわけである。

台形公式の局所誤差は であり、中点公式と同じである。2点も使っ て、1点しか使わない中点公式と同じでは意味がないと思う人もいるかもしれ ないが、実はそうでもない。1区間だけを考えるとたしかに台形公式は2点使う が、ある区間の左端はもちろんその左の区間の右端なので、関数の値は同じだ からである。つまり、全体をn個の区間に分けた時、中点公式では n回関 数を計算するが、台形公式ではそれより1多い n+1回計算するだけである。

区間の端ではない、一般的な位置に点をとるとすればどうであろうか？以下、 面倒なので区間 で級関数

の積分をするということにする（適当な変数変換をすればいつでもこう置き換 えられる)。

積分した結果は

となって、テイラー展開の偶数項しか現れないことに注意して欲しい。

2点の x座標を と 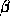としたとき、一般的には数値積分の近 似式が

の形になる。これで、上の積分を近似するわけだが、0次の項が消えるために , また奇数次の項が出てこないために かつ である必要があることは すぐにわかるであろう。

というわけでと決まってしまったので、あと 出来ることは の値を決めることだけである。式 7を書き直すと

となるので、

とすれば、までの項を一致させられるということがわかる。

台形公式は に相当し、 までしか消えていないので、ずいぶ ん精度が上がっていることがわかるであろう。 そのかわり、区間の端の点の再利用が出来ないので、中点公式に比べて計算量 が2倍になっているということに注意しておく。

もうちょっと頑張って3点にしてみよう。等間隔に点をとるなら両端と中点 であり、このときは2次曲線で近似して局所誤差は3次となる。これはいうまで もなくシンプソンの公式である。

不等間隔の時何が実現できるかだが、ここでは具体的に形を書かない。2点の 場合と同様な考察から、区間の中点を1つ、両側に1点づつとると、こんどは までの項を一致させられるということがわかる。

ここまでの話だと、

• 両端を含むn点の等間隔補間で積分公式を作ると、n-1次の多項式近似になっ て局所誤差は n次
• 不等間隔で積分公式を作ると、なんだかよくわからないが2n次

1.2 ガウス型公式の次数

前回の資料の最後に書いたように、ガウス型（あるいは、ガウス・ルジャンド ル型）積分公式は、ルジャンドル多項式の零点を点にとるものである。ルジャ ンドル多項式は有限区間 で与えられる直交関数系である。そのk番 目の項はk次多項式であり以下の性質を持つ。

定義はいろいろあるが、

と書かれることが多い。

の零点とは、の解のことである。n次ルジャンドル多項式の場合 実区間にn個必ず零点がある。これを以下 と する。

さて、以下でガウス型公式の次数について考える。n点使った時に2n次 になる、いいかえれば 2n-1次までの多項式については厳密な値を与えると いうことが予想されるので、これを示すという方針で考えていく。

任意の 2n-1次多項式 に対して、の全ての零点で値が 一致するようなn-1次多項式 を構成することができる。これを 使うと、

と書ける。ここで、 は n-1次の多項式である。これを区間 で積分すると、もちろん

であるが、右辺の第一項の は n-1次多項式であり、n次ルジャ ンドル多項式 は n-1次以下の任意の多項式と直交するので、この積分 は0になる。つまり、

となるわけである。というわけで Fの積分を計算するには Lの積分を求めれ ばいい。ところが、 L は n-1次なので、 n 点での値が決まれば一意に 決まり、積分出来てしまう。

結局、 の零点での値を使えば、 の積分が計算できたことに なる。

さらに厳密な話としては、 2n-1次よりも高次の項がある関数を近似して積 分したときにどのような誤差項が入ってくるかという議論が必要になるが、こ れは省略する。

一般に、特異点を持たないような性質のよい関数の時には、ガウス型積分公式 は非常に強力な方法であるといえる。

なお、一般の次数の場合、ガウス型公式は

の形をとる。これらの定数の値については適当な参考書を見ること

1.3 微分方程式への積分公式の適用

さて、ここまで数値積分の話をしたわけだが、微分方程式の数値解法と数値積 分はもちろん非常に良く似たものである。が、大きな違いは、数値積分では被 積分関数が

と、独立変数の陽な関数として与えられていたのに対し、微分方程式では

と積分された結果自体に被積分関数がよっていることである。このために、話 がすこし複雑になる。

例えば、もっとも簡単な中点公式の場合を考えてみよう。数値積分の場合には、 単に

であった。微分方程式の場合、問題は での x の値を我々 はまだ知らないということである。

この困難は、数値積分が近似多項式の積分として与えられたということを思い 出せば一応解決できる。中点公式の場合、数値積分ではこれはfを で近似するということに相当した。同様なアイディアを微分 方程式に適用すれば、微分方程式の場合、 fを定数で近似し、その結果解で ある x を一次式で近似する、つまり

という近似をする。これから、問題の中点での値を と書くと

と書けるわけで、これは に対する代数方程式になっている。これを 解けば数値解も求まるわけである。

一般には、n次のルジャンドル多項式から導かれる公式では、fの n-1次 近似多項式を構成することになる。これを前節と同様 とし、零点を とすれば、での「解」 が

がなり立ち、さらに

がなり立つように と L を決め、それを積分して での解が求 まるということになる。

と書くと非常に大変そうだが、係数をあらかじめ計算しておけば上の手続きが 陰的ルンゲクッタ公式として表現できる。これで、例えば 4 段で 8 次の公式 が実現出来るわけである。

1.4 代数方程式の扱い

さて、上のようなわけで陰的公式というものが構成できるということはわかっ たが、これを実際に使うには、 に対する代数方程式をとかないといけ ない。この解き方について簡単に説明しておこう。

代数方程式といっても、ここで扱うものはほとんど必ず

の形、すなわち、ある関数の不動点を求めるという形になっている。この時は、 以下のような反復を繰り返すことによって解くという方法が考えられる。

これを直接代入法という。

これは容易にプログラム出来て、実際に広く使われる方法である。が、理論的 にはいろいろ怪しい。つまり、

• 収束するかどうか
• 収束の速さ

しかし、陰的ルンゲクッタから出てくる方程式の場合、これで結構うまくいく ことが多い。それがなぜかということを示す前に、一般に直接代入の収束の速 さを調べておこう。

方程式(23)の解が x であるとき、 直接代入法での古い近似 解と新しい近似解それぞれの真の解との差は

となる。下の方を変形し、fを展開すれば

となる。従って、

• 収束するためには であればよい。
• が小さいほど速く収束する。

話を陰的ルンゲクッタに戻そう。

また、もっとも簡単な中点公式（陰的中点公式）で考えてみる。 解くべき式は、 として

と書ける。 例によってリプシッツ連続条件

がなり立つとしてよいので、中点公式28の右辺の x による微分が で押えられるということがわかる。つまり、刻み 幅を に比べて小さくとればいいということになる。

なお、これでは済まないような場合もある。これについては後の「硬い」方程 式のところで扱うことにする。

1.5 ガウス型以外の陰的公式

陰的ガウス公式は、段数に対して理論上可能な最大次数を達成する、ある意味 で「最良」の公式である。が、実用上はいろいろ不便な点もある。例えば、

• 最 小の段数で最高の次数（精度）を達成しているので、係数に自由度がなくいわ ゆる「埋め込み型」の公式が構成できない。
• 端の点を使わないので、前 のステップでの計算結果の再利用が出来ない。
• 完全陰的法なので、計算が大変である