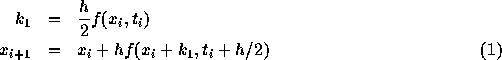
資料の番号と講義の進み方に若干ずれが生じているが、資料のほうは先に進め ていくことにする。今回は、 Runge-Kutta 法についてその考え方を説明して いこう。
2次の Runge-Kutta 法とは、以下のようなものであった。
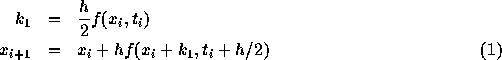
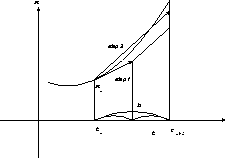
これについては、図的な説明というものが可能である。元の点からまずオイラー
法と同様に接線を引く。が、これを次の時刻まで延ばすのではなく、ステップ
の半分のところで止める。で、ここでもう一回微分方程式の右辺を評価する。
ここでの導関数の値を使って、もとのところ 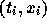 から直線を引くわ
けである。
から直線を引くわ
けである。
実は、2次精度を実現する RK型の公式というのはこれ一つではない。以下のよ うなものも可能である。
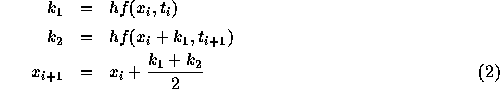
さらに、これらの公式を含む一般的な公式を与えることもできる。
今日は、まず、RK法というものの一般的な定義を与え、それからどのようにし て上の公式が得られるかを考える。また、そこからさらに高次(高精度)な公 式の導出につなげていこう。