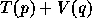さて、 leapfrog 公式は、上で見たようにハミルトン系に対してエネルギー誤 差が有界に留まるという大きな特長がある。が、2次精度でしかない。もっと 高次の方法はないのだろうか、またあるとすればどういう原理で作れるのだろ うか。
高次の方法を構成する一つのアプローチが、シンプレクティック公式といわれ るものである。これはなにかというと、積分公式がシンプレクティック写像に なるように作るということである。
と、これでは意味がわかりませんね。シンプレクティック写像とは、ようする に正準変換のことである。正準変換とはなにかというのは解析力学の入門書を みて欲しいが、直観的には、力学系を不変に保つ、つまり変換まえの座標系で 求めた軌道を変換したものと、変換後の座標系での力学系の軌道が厳密に同じ になるようなものである。
ハミルトン力学系の解そのもの（ある時刻 t での座標から、 t+h での座 標に移す変換）もシンプレクティックである。まあ、だから、シンプレクティッ クになっているような積分公式は、そうでないものに比べてなんとなく力学系 の性質にあっているような気はする。
で、いいたかったことは何かっていうと、上の leapfrog 公式はこのシンプレ クティック性を満たしているということだった。詳しくは、「数理科学」 1995年6月号にのった吉田による解説記事でもみてもらうことにして、ここで は高次の公式にはどんなものがあるかという話をしておく。
陽解法の組み立て方はいろいろある。一つは、 RKN 系の公式で、係数をシン プレクティック性を満たすように決めるということである。これはここ10年で 無数に論文がでた。4次、あるいは6次の公式としては、吉田や鈴木による作用 素分解に基づく公式が良く知られている。
これらの方法の原理は、要するに上の leap frog をタイムステップを変えて いくつか組合わせるというものである。うまくタイムステップを組み合わせる と誤差の高次の項を消すことができるわけである。3段4次の公式、7段6次の公 式等が吉田によって導かれている。
なお、実は陽解法はハミルトニアンが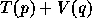 
の形の場合にしか使え
ないが、大抵の問題はこう書けることはいうまでもないであろう。
また、 RKN 系の公式を力任せに構成する試みもあり、4次から8次までの公式 が作られている。計算精度という観点からはこちらのほうが leapfrog を組合 わせるものよりも圧倒的にいいということがわかっている。
陰的ルンゲクッタについては、係数がある特別な条件を満たせばシンプレクティッ クになるということがわかっている。いろいろな公式が知られているが、特に 今まで何度もでてきた陰的ガウス法が次数に無関係にシンプレクティックであ るということがわかっている。これは他の観点からも「最良」な公式であるの で、それ以外の方法を使う必要はそれほどないであろう。なお、ハミルトン系 は普通 non-stiff なので、逐次代入法で収束させることができ、収束も速い。
さて、シンプレクティックであるということと、「良い」ということの間には
ちゃんとした理論的な関係があるのであろうか？一応あるということになって
いる。つまり、あるハミルトニアン H で表される系をシンプレクティック
な p 次の公式を使って積分した解は、別のハミルトニアン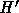 
で与えられ
るシステムの厳密解になっていて、H と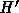 
の間に
という関係がある（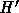
を求める数列が収束すれば）ということがわかってい
る。
なお、例えば上の調和振動子の場合には実際に数列が収束し、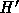
が求まっ
ている。が、これは極めて例外的な場合で、一般の場合には収束するかどうか
も明らかではないようである。
収束するかどうか明らかではないのでは、使っていいことがあるという保証は ないではないかと思うかもしれない。理論的にはその通りなのであるが、実際 にはいろいろな問題に適用されて、従来の方法よりも高い精度が得られるとい うことが確認されている。
