
ハミルトン系の安定性とかいっても、一般的な議論がそんなにできるわけでは なくて、多様な数値積分法に対する安定性のちゃんとした解析が出来ているの は結局線形の問題(調和振動)の場合ということになる。というわけで、まず、 調和振動の場合の理論の枠組について説明しておこう。
まず、先週紹介した対称型多段階法について、線形安定性の意味をあきらかに しておこう。一階の方程式の場合には、線形安定性とは線形方程式の解がいつ かは原点に向かうこと、つまり、線形の方程式に対応する差分方程式の解の実 部が負であるということであった。
しかし、ハミルトン系の場合にはこれが数値解がもとの解を表現しているとい うことの適切な条件とはいい難いというのはすでに述べた通りである。という のは、調和振動の場合では明らかなように、真の解というのは無限に振動が続 くのに対し、線形安定性の意味で安定な数値解は原点にむかって落ちていくこ とになるからである。このため、例えばエネルギーは保存し得ない。
というわけで、調和振動の方程式

に、(2階の方程式用の)多段階法
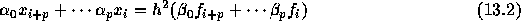
を適用した場合の解について考えてみる。今、

とおけば、数値解法から得られる差分方程式は

と書くことができる。この差分方程式の一般解は、
ここで、  は代数方程式
は代数方程式
の解であり、 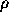 と
と  はそれぞれ第一特性多項式、第二特性多項
式とよばれるものであり、定義は
はそれぞれ第一特性多項式、第二特性多項
式とよばれるものであり、定義は

である。なお、面倒なので方程式(13.6) は重根を持たない ということにしておく。
さて、一般解が (13.5)の形で与えられるというこ とは、つまり、数値解が一定の振幅で振動を続けるための条件は、方程式 (13.6) のすべての解の絶対値が 1 に等しい、つまり

ということである。そんな都合のいいことが本当にあるのだろうか?
というわけで、例によって leap frog 公式

に適用してみることにする。

となるので、  とおけば、方程式(13.6) は
とおけば、方程式(13.6) は

となる。これについては、すぐにわかるように複素数解の絶対値はかならず 1 なので、解の絶対値が 1 である条件というのは単に複素数解をもつ条件 ということになり、少し計算すれば

であればよいということがわかる。つまり、  ということ
である。従って、周期の 1/3 より少し小さいくらいの刻み幅をとっておけば、
解が振動的であるという性質が保存されているということがわかる。
ということ
である。従って、周期の 1/3 より少し小さいくらいの刻み幅をとっておけば、
解が振動的であるという性質が保存されているということがわかる。
なお、上の、解の絶対値が 1 であるような Hの領域を、周期性区間 interval of periodicity という。
さて、線形安定性の時に A-安定性という概念を導入したように、周期性につ いても同様なことが考えられよう。つまり、周期性区間が非負の実数軸全体を 含むということを特に P-安定であるという。P-安定についても、A-安定と 同様なダールキストによる以下の結果が知られている:

これは実は台形公式である。
さて、P-安定な公式というのは台形公式だけなわけだが、実用上は P-安定で
なくても、周期性区間が極端に小さくなければ使えるであろう。つまり、 H
の最大値が解の周期に対して周期性をたもつ最大のステップの大きさを与える
ので、まあ、それが存在して極端に小さくなければいいではないかということ
になる。そのような、有限の周期性区間をもつ線形多段階法をつくる方法とし
て現在のところ唯一しられているのが、前回出てきた対称型公式である。
Quinlan & Tremaine に従って概要を説明すると、 数値解が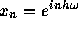 の形をしているとして、 これが従う方程式はもちろん
の形をしているとして、 これが従う方程式はもちろん

となるが、右辺の分母分子に  を掛けてみると、対称型
公式で
を掛けてみると、対称型
公式で  とかの性質があると、ちょうどそれらの
項の虚部が打ち消し合うので、結局任意の
とかの性質があると、ちょうどそれらの
項の虚部が打ち消し合うので、結局任意の  について右辺が実数とい
うことになる。
について右辺が実数とい
うことになる。
あとは、実際に値が正であれば、周期性区間に入っているということになる。
周期性区間がどこまでであるかというのは、公式を決めて数値計算してみない とよくわからない。これについてはまだそんなに研究されていなくて、最近福 島によって系統的な研究がでたばかりである。
福島の結果では、陽公式の場合には周期性区間を大きくすると誤差定数が大き くなってしまう。が、陰公式ではそのような問題はなく、次数に無関係に周期 性区間が1 程度あるものが見つかっている。
さて、ルンゲクッタの場合にも、上と全く同様に周期性区間とか P-安定性と かを考えることができる。もうそれほど驚くべきことではないと思うが、例に よって以下のようなことがわかっている
なお、陰的ガウス法以外にもP-安定な公式は知られているが、ここでは紹介し ない。