これまで何度か強調してきたように、無衝突ボルツマン方程式 CBE で記述さ れるシステムの力学平衡状態は熱平衡ではないし、自己重力系は熱平衡ではあ りえない。しかし、 King model のように近似的に熱平衡なものもあるので、 ここでエネルギーの出入りに対する系全体の応答、つまり比熱というものをちょっ と考えてみることにする。
ビリアル定理から ![]() であったので、すぐにわかるように「エネルギー
を奪うと運動エネルギーが増え、逆ならその逆になる」ということになってい
る。つまり、見かけ上比熱が負になっている。
であったので、すぐにわかるように「エネルギー
を奪うと運動エネルギーが増え、逆ならその逆になる」ということになってい
る。つまり、見かけ上比熱が負になっている。
これは重力が効く系では普通のことで、例えば地球を回る人工衛星といったも のでも同様のことが起こっているわけである。
この、「見かけ上比熱が負」ということが、熱力学的不安定を通して構造形成 (自己組織化)が起きる基本的な理由である。
まず、系の「大きさ」についてどんなことがいえるかということをおさらいし
ておく。![]() は全ポテンシャルであったので、定義により以下のように書ける:
は全ポテンシャルであったので、定義により以下のように書ける:
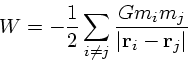 |
(35) |
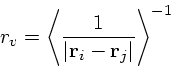 |
(36) |
 |
(37) |
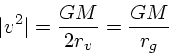 |
(38) |
大雑把な見積りでよければ、例えばhalf mass radius (質量の半分が入って
いる半径)![]() を適当に見積もって、それで
を適当に見積もって、それで ![]() の代わりにしてもそれほど大
きな誤差はない。典型的には
の代わりにしてもそれほど大
きな誤差はない。典型的には
 |
(40) |
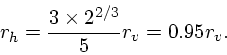 |
(42) |
今、![]() 軸まわりに対称な、回転している銀河を考えると、ポテンシャルテン
ソルについては対称性から
軸まわりに対称な、回転している銀河を考えると、ポテンシャルテン
ソルについては対称性から
| (43) |
| (44) |
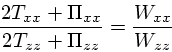 |
(45) |
 |
(46) |
| (47) |
| (48) |
 |
(49) |
さて、 ![]() と、銀河の「形」の関係についてであるが、一般に密
度が以下のように書ければ
と、銀河の「形」の関係についてであるが、一般に密
度が以下のように書ければ
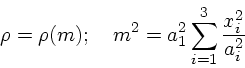 |
(50) |


まあこんな感じになる。上の図は、 ![]() の関数として
の関数として
![]() がどう変化するかを、
がどう変化するかを、 ![]() のいくつかの値について示したも
のである。破線は、真横でない方から見たらどういうふうになるかを、いくつ
かの場合について示したものである。下の図は、実際の観測結果と
のいくつかの値について示したも
のである。破線は、真横でない方から見たらどういうふうになるかを、いくつ
かの場合について示したものである。下の図は、実際の観測結果と ![]() の線を重ねて書いてみたものである。暗い楕円銀河は
の線を重ねて書いてみたものである。暗い楕円銀河は ![]() の線
に近いところに集まっているのに対し、明るいものは可能な範囲全体にあり、
どちらかというと下の方(回転が小さく、おそらく異方性が大きいほう)に集
まっているということが見てとれる。このような構造の違いは、それぞれの銀
河がどうやってできたかということになにか重要な手がかりを与えているはず
である。
の線
に近いところに集まっているのに対し、明るいものは可能な範囲全体にあり、
どちらかというと下の方(回転が小さく、おそらく異方性が大きいほう)に集
まっているということが見てとれる。このような構造の違いは、それぞれの銀
河がどうやってできたかということになにか重要な手がかりを与えているはず
である。
とはいうものの、どうやってできたかということに対する標準的な理解という ものがあるわけでは必ずしもない。ここでは、せっかくなので一つの考え方と して、合体説(楕円銀河のうち、特に大きいものは銀河同士の合体でできた) をとった場合にはどのような説明が可能かということを見てみる。これ以外の 解釈がないというわけではない。

これは Okumura et al. (1991, PASJ 43, 781) によるシミュレーショ
ンの結果と上のグラフを重ねたものである。シミュレーションはすべて2つの
等方的で回転を持たないプラマーモデルを2つ放物軌道でぶつけたもので、番
号順に最初の軌道の近点距離が大きくなる( 4 で ![]() である)。
である)。
大雑把にいうと、番号の大きいものほど軌道角運動量が大きいので、
![]() が大きくなる。もっとも、ある程度より大きくなっていないこ
とに注意してほしい。これは要するに合体するためにはかなりの軌道角運動量
を捨てないといけないので、残った系が持つ角運動量には上限があるためであ
る。
が大きくなる。もっとも、ある程度より大きくなっていないこ
とに注意してほしい。これは要するに合体するためにはかなりの軌道角運動量
を捨てないといけないので、残った系が持つ角運動量には上限があるためであ
る。
合体後の銀河は特別な場合(1,7)を除いて3軸不等なので、その3方向からみ てグラフ上に点をとり、それを結んで3角形を書いている。大雑把にいって、 適当な方向からみたときにはこの3角形の中にあると思っていい(実際にある 方向から見た時にどう見えるかというのはもうちょっとややこしいが、いまは そのあたりの議論は省く)。
シミュレーションの結果からわかることは、仮に楕円銀河が合体で出来たとす れば、暗いものは初期に近点距離の大きな軌道(おそらく楕円軌道)をもち、 明るいものは近点距離の小さな軌道から合体したものが比較的多いということ になろう。
まあ、もうちょっと素直な解釈は、暗いものは合体ではなく、円盤銀河からガ スがなくなったり円盤が摂動を受けて厚くなったりしてできた、というものか もしれない。