中心にブラックホール(というか、なんか重いもの)がある星団ではどの ような構造が見られることになるだろうか?これに理論的に答えたのは Bahcall and Wolf (1978) である。この頃には球状星団の中心にブラッ クホールがある可能性がかなり高いと考えられていたため、そのような方向の 研究が盛んであった。しかし、 球状星団の X 線源がほとんど Low-mass X-ray binary、つまり中性子星と小さな主系列星の連星であり、また必ずしも 星団中心にあるわけでもないということが 1980年代になって明らかになった ため、しばらくこの方向の研究は止まっていた。
それはともかく、Bahcall and Wolf はフォッカープランク方程式を数値的に 解くことで密度構造を決めたが、その結果は解析的に理解できることがわかっ ている。その考えは以下のようなものである。
中心部分の、ブラックホールの重力が支配的な領域を考え、また簡単のために
分布関数は等方的であるとする。 速度分散はポテンシャルで決まるので、ケ
プラー速度になって速度は
![]() になる。密度が
になる。密度が ![]() であるとしよう。
であるとしよう。
中心に向かって温度があがっているので、熱は中心から外側に向かって流れる。
ここで、定常状態ならば熱流 ![]() が半径に依存しない。
が半径に依存しない。
大雑把にいうと、ある半径での熱流は、そこでの緩和時間くらいの間にその領 域の全エネルギーぐらいが流れ出すと考えることで見積もることができる。こ れはなんか根拠がない仮定であると思うかもしれないが、仮に密度が半径のべ きであるとすれば、 温度は元々半径のべきなので無次元量としての温度勾配 の大きさはどこでも同じになるため、この仮定は正しいことになる。
問題は、ではそういうべき乗の解はあるかどうかということだが、緩和時間は
![]() の程度、全エネルギーは
の程度、全エネルギーは
![]() の程度なので、
の程度なので、 ![]() と置くことで
と置くことで
| (1) |
こんな大雑把な計算でいいのかと思うであろうが、割合うまく数値計算の結果 を説明できている。
ここまでは中心にブラックホールがある系について、周りにあるのが同一の質
量の星の集団であり、熱力学的な定常状態になれば密度が半径の ![]() 乗の
べき分布になることを導いた。これは理論的には美しいが、必ずしも非常に現
実的なケースとはいいがたい。以下では、より現実的と考えられるいくつかの
場合について、分布がどのようになるべきかを考えてみる。具体的には、以下
の 3 ケースを考える
乗の
べき分布になることを導いた。これは理論的には美しいが、必ずしも非常に現
実的なケースとはいいがたい。以下では、より現実的と考えられるいくつかの
場合について、分布がどのようになるべきかを考えてみる。具体的には、以下
の 3 ケースを考える
これらはそれぞれ、対応する現実的な系がある(かもしれない)と考えられる。
これは、例えばガス降着などでブラックホールが比較的ゆっくり成長する場合 に、周りの恒星集団の分布がどう変わるかという話である。ゆっくりといって も、力学的な時間スケールよりは十分に遅いが2体緩和の時間スケールよりは 速いものを考える。これは、銀河中心の巨大ブラックホールの場合にはありそ うな話である。
QSO や AGN のcentral engine は巨大ブラックホールへのガス降着であると考 えられているので、ガス降着が終わったあとの恒星系の分布は、この、ブラッ クホールが断熱成長した場合で与えられると考えられるであろう。この場合の 分布関数の変化を数値的および解析的に調べたのは Young (1980, ApJ, 242, 1232) である。以下、彼の論文の議論を要約しよう。
始めはブラックホールがなかったとして、分布関数が ![]() であるとする。
考えないといけないことは以下の2つである。
であるとする。
考えないといけないことは以下の2つである。
というわけで、順番に考えていこう。
まず、![]() にいた星ががどこに移動するかであるが、 ポテンシャルは球
対称のままなのでその形が変化しても角運動量
にいた星ががどこに移動するかであるが、 ポテンシャルは球
対称のままなのでその形が変化しても角運動量 ![]() は保存する。従って、
は保存する。従って、
![]() の変化だけを考える。 ポテンシャルの変化はゆっくりであるとしたので、
断熱不変量がある、具体的には、 radial action
の変化だけを考える。 ポテンシャルの変化はゆっくりであるとしたので、
断熱不変量がある、具体的には、 radial action
![\begin{displaymath}
I_R = \oint v_r dr = 2\int_{r_-}^{r_+} [2(E-\phi)-(J/r)^2]^{1/2}dr
\end{displaymath}](img13.png) |
(2) |
初めに恒星系は有限サイズのコアを持っていたとしよう。この時、コアの十分
内側では、 ポテンシャルは中心密度を ![]() として
として
| (3) |
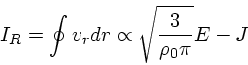 |
(4) |
| (5) |
さて、問題は、 ![]() がどうなるかであり、これがわかれば密度分
布がわかる。少しややこしいのは、最初のエネルギーが同じであっても最終の
エネルギーは角運動量
がどうなるかであり、これがわかれば密度分
布がわかる。少しややこしいのは、最初のエネルギーが同じであっても最終の
エネルギーは角運動量 ![]() によって違うことで、このために算数が少し面倒
になる。
によって違うことで、このために算数が少し面倒
になる。
分布関数 ![]() ではなく、
ではなく、 ![]() 空間での分布関数
空間での分布関数 ![]() を考えると、
ブラックホールの成長によってこれは滑らかに射影されるので
を考えると、
ブラックホールの成長によってこれは滑らかに射影されるので
| (6) |
| (7) |
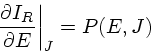 |
(8) |
 |
(9) |
後は ![]() と
と ![]() の関係だが、これは単に
の関係だが、これは単に
| (10) |
| (11) |
つまり、ブラックホールが恒星系の中心で断熱的に成長する場合には、ブラッ
クホールの十分近くでは
![]() のカスプができることに
なる。
のカスプができることに
なる。
これは美しい理論であり、また重要な結果でもあるが、直接に天文学的な応用
があるかと言われると難しい。ブラックホールがあるという観測的な傍証があ
るのはおもに巨大楕円銀河と近傍の円盤銀河であるが、どちらも中心スロープ
が ![]() とは遠く離れているからである。
とは遠く離れているからである。
具体的には、巨大楕円銀河ではスロープが非常に浅く、 ![]() から
から ![]() 程
度の範囲に分布する。これに対して、我々の銀河系や近傍の円盤銀河では、
程
度の範囲に分布する。これに対して、我々の銀河系や近傍の円盤銀河では、
![]() 的と考えられている(我々の銀河系でもブラックホールに本当に近い、距
離にして 1 pc くらいのところなのでなかなか良くわからないが)。
的と考えられている(我々の銀河系でもブラックホールに本当に近い、距
離にして 1 pc くらいのところなのでなかなか良くわからないが)。
巨大楕円銀河でカスプが非常に浅いことは、ブラックホール、巨大楕円銀河の
起源を考える上では大きな問題である。もしも、 QSO が巨大楕円銀河の直接
の projenitor であって、 QSO のガスが無くなって静かになったものが巨大
楕円銀河であるとするなら、ブラックホールの周りの恒星の分布は ![]() 乗
カスプになりそうなものだからである。
乗
カスプになりそうなものだからである。
それ以前に、そもそも ![]() よりも浅いカスプを作る方法はあるのかというの
も問題である。
よりも浅いカスプを作る方法はあるのかというの
も問題である。
ここまでは、
を考えた。もうひとつの可能性として、力学的な時間スケールでブラックホー ルが形成されるか、あるいは系の中心以外のところから落ちてくることが考え られる。
力学的な時間スケールで巨大ブラックホールを成長させるには、宇宙初期のゆ らぎから重力不安定で一気に作るという方法もありえる。しかし、現在の標準的な インフレーション宇宙モデルでは最初に重力不安定からコラプスする質量スケー ルはかなり小さく、その中のバリオン質量はもっと小さいので巨大ブラックホー ルを一気に作るのは無理がある。
現実的な階層的な構造形成モデルを考えると、大きな銀河はより小さな銀河が 合体することで形成されたということになる。この時に、銀河中心にあるブラッ クホールには何が起きるだろうか?、また、銀河の中心部の構造はどうなるの だろうか?
銀河同士の合体は、前に議論した「激しい緩和」の典型であり、十分に緩和が 進む前に構造が固まってしまう。ブラックホールが中心にある場合、これは、 合体してもブラックホールは初めから結構中心近くに行くということである。
まず、合体前の銀河がほぼ自己重力的でブラックホール質量よりも大きなコアを持っ ていた場合を考える。この場合には、コアは合体の時に大きく構造が変化する が、ブラックホールはコアの中ないしは非常に近くにいるであろう。ブラック ホールは回りの星よりも圧倒的に重いので、力学的摩擦によりコア中心に沈む。 2つブラックホールがあればそれらは連星になり、しばらくは回りの星をはね 飛ばして進化する。
合体前の銀河がコアをもたず、
![]() ないしはそれより急な
ハローから、ブラックホールの重力が支配的な領域に滑らかにつながった構造
をしている場合も、合体中にブラックホールはほぼ中心まで沈み、2つあれば
連星ブラックホールになって近くの星をはね飛ばすことになる。
ないしはそれより急な
ハローから、ブラックホールの重力が支配的な領域に滑らかにつながった構造
をしている場合も、合体中にブラックホールはほぼ中心まで沈み、2つあれば
連星ブラックホールになって近くの星をはね飛ばすことになる。
今、ブラックホール以外は無衝突系である極限的な場合を考えると、ブラック ホール連星は合体してできた銀河の中心にいって、重心運動の速度は 0 になっ て止まっている。ブラックホール連星の軌道長半径程度まで近づいた星は基本 的にははね飛ばされて無くなるので、ある程度よりもエネルギーが低い粒子は 存在しないことになる。細かいことをいうとはね飛ばされる条件はエネルギー ではなく近点でのブラックホールからの距離だが、とりあえずエネルギーに下 限がある場合を考える。
この時には、簡単な議論から中心に
![]() のカスプがで
きることがわかる。以下、 Nakano and Makino (1999, ApJL 525, 77) に従っ
てこのことを示す。
のカスプがで
きることがわかる。以下、 Nakano and Makino (1999, ApJL 525, 77) に従っ
てこのことを示す。
分布関数がエネルギー![]() だけの関数だ
とすると、ある半径
だけの関数だ
とすると、ある半径 ![]() での密度は
での密度は
ブラックホールに十分に近いところでは、ポテンシャルが十分に深いとすると、
積分区間の下限は ![]() だが、そこに来る前に
だが、そこに来る前に ![]() は 0 になるので
上の式は
は 0 になるので
上の式は
![\begin{displaymath}
\rho(r)=4\pi \int^{0}_{E_0} f({E}) \sqrt{2\left[%%
{E}-\phi(r) \right]} d{ E},
\end{displaymath}](img49.png) |
(13) |
![$\displaystyle 4\pi \int^{0}_{\cal E_{\rm0}} f(E) \sqrt{2\left[%%
E-\phi(r)\right]} d{ E}$](img54.png) |
|||
![$\displaystyle 4 \sqrt{-2\pi \phi(r)}
\int^{0}_{ E_{\rm0}} f( E) \left[%%
1-\fra...
...}{\phi(r)}+O\left({\left[\frac{{
E}}{\phi(r)}\right]}^{2} \right) \right] d{ E}$](img55.png) |
|||
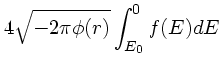 |
(14) |
| (15) |
 |
(16) |
この結果は、本質的には
という 2 つの仮定だけによっているので、割合に一般性が高いと考えられる であろう。
とはいえ、上の仮定は結構強い仮定なので、実際に成り立つか?という問題は ある。まず、数値計算ではどんな風かというのを見てみよう。この辺は信用で きる数値計算結果はあまりないので、手前味噌になるが Makino and Ebisuzaki 1996 (ApJ 465, 527) を例にしよう。
図に、中心ブラックホールを持つ銀河(左)ともたない銀河(右)について、合体 したものを種にしてまた合体させるということを繰り返した時に密度プロファ イルがどう進化するかを示す。合体する毎に半径はほぼ2倍になるが、この図では横軸をスケールして重なるようにしている。
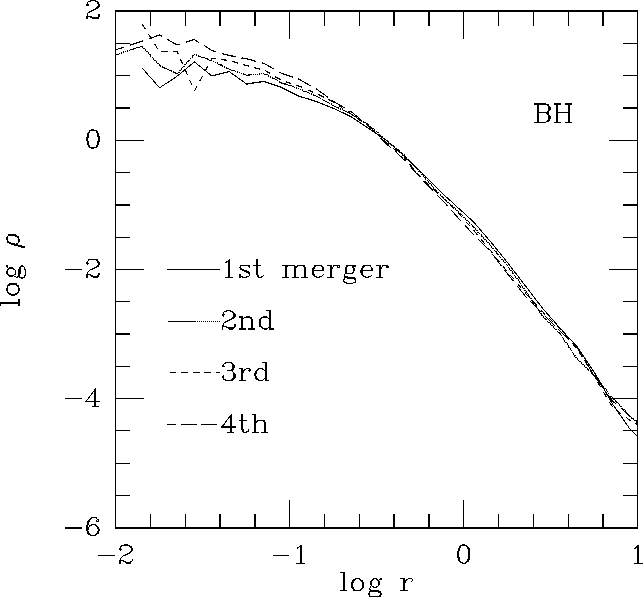
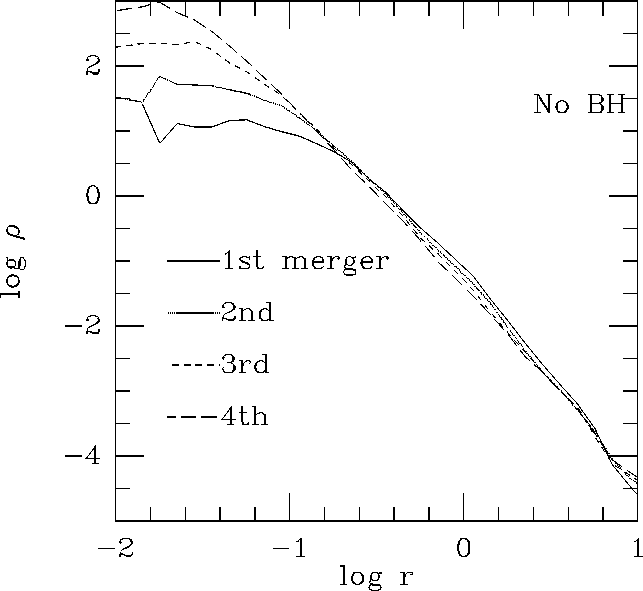
ブラックホールがある場合だと、合体を繰り返した時に中心に浅い密度カスプ
が形成され、その領域の銀河の半径に比べた相対的な大きさはほぼ一定になっ
ていることがわかる。この部分の傾きはほぼ ![]() であり、 Nakano and
Makino の理屈の通りになっているといえる。
であり、 Nakano and
Makino の理屈の通りになっているといえる。
まあ、論文の出版年から想像されるように、 Makino and Ebisuzaki は「結果 はこうなった」と書いているだけでなぜそうなるのかという説明は Nakano and Makino までちゃんとはなかったわけである。こういうは本当はよろしく ないという考え方もある。というのは、特に定性的な結果については、数値シ ミュレーションが正しいか間違っているかということの判断は、解析的な解釈 がつかない限り一般には非常に難しいからである。 NFW プロファイルの話の 時に議論したように、ユニバーサルな結果と思ったものが、ユニバーサルに計 算間違いしていたせいということもある。
ブラックホールがある銀河の合体の、この数値シミュレーションについては、
やった人は計算の信頼性についてはそれなりの自信があったわけだが、
Nakano and Makino の結果がでて初めて確信を持ってスロープが ![]() にな
るといえるようになった。
にな
るといえるようになった。
観測はどんな風かというと、想像されるように数値シミュレーションほど綺麗 になにかが決まるわけではない。が、まあ、傾向はある。
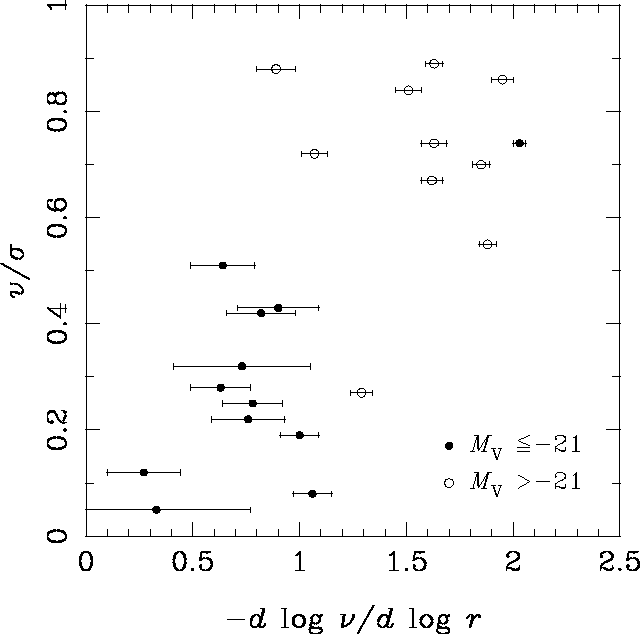
明るい楕円銀河はスロープが ![]() よりも浅く、回転が小さいのに対して、暗
い楕円銀河がスロープが
よりも浅く、回転が小さいのに対して、暗
い楕円銀河がスロープが ![]() 近くであり回転が卓越しているという傾向がか
なりはっきりあることがわかる。
近くであり回転が卓越しているという傾向がか
なりはっきりあることがわかる。
3 次元に密度を deprojection する時の誤差等の見 積もりに問題がある可能性がまだなくはないようだが、定性的に明るい銀河が 浅いスロープを持つという結果自体は確実なものといえるであろう。
最後に、「現在の球状星団の中心にブラックホールがあるとすればどんなふう に見えるはずか」という問題についてちょっと考えておこう。
2回前に話をしたように、現在 core collapse をしている球状星団では中心に ブラックホールが形成されるということはありそうにない。 が、球状星団が 生まれた直後の大質量星がある時には暴走的な合体から中質量ブラックホール が形成された可能性はある。
その後現在まで進化したら球状星団はどのように見えるか?というのがここで
の問題である。単純に考えると、前回話をしたようにブラックホールの近くで
の密度分布は ![]() 乗のカスプになると考えられるが、これは等質量の星だ
けを考えた場合である。ブラックホールの存在を考えない、 gravothermal
catastrophe の場合には、シミュレーションでは中性子星や重い白色矮星は理
論通りのほぼ
乗のカスプになると考えられるが、これは等質量の星だ
けを考えた場合である。ブラックホールの存在を考えない、 gravothermal
catastrophe の場合には、シミュレーションでは中性子星や重い白色矮星は理
論通りのほぼ ![]() 乗のカスプを作るが、見える星はもっと軽いためにもっ
と浅いカスプになるというのは既に見た通りである。
乗のカスプを作るが、見える星はもっと軽いためにもっ
と浅いカスプになるというのは既に見た通りである。
ブラックホールがある場合にも同様に、中性子星や重い白色矮星はほぼ理論通りの カスプを作るが、見える星はずっと浅いというのが最近のシミュレーションの 結果(Baumgardt et al. 2004) である。
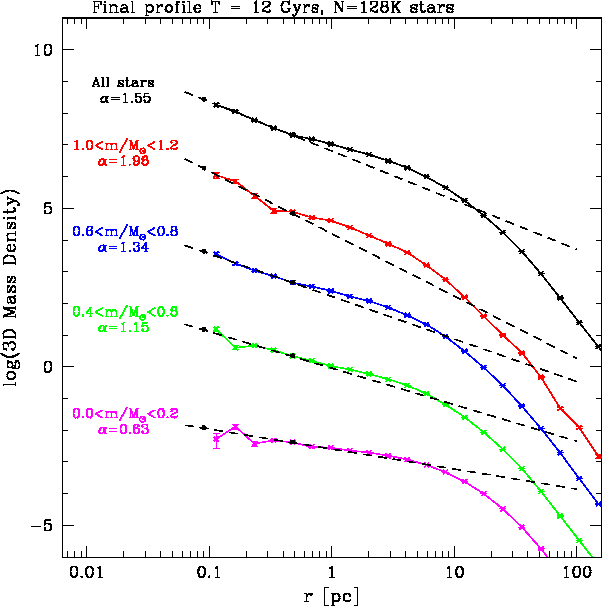

上の図は3次元的な密度分布を星の質量毎に書いたものである。初期条件はか なり深いキングモデルの中心にブラックホールをおいたものである。
ブラックホールの近くではどの質量でもカスプになっているが、そのスロー プは質量が小さいと小さくなることがわかる。明るい星 (turn-off mass の辺 り)の分布を2次元に投影したのが下の図で、基本的にフラットなコアを持つ 「普通の」キングモデルでフィットできる球状星団のように見える。
というわけで、この辺はまだ 100% 信用してもらっても困るが、球状星団の中心 にブラックホールがあるとすれば、その球状星団は比較的大きくフラットなコ アを持つように見えるということになる。