Subsections

• 1.1 ガスと$N$体の違い

1 有限振幅での進化

前回は、断熱壁に囲まれた自己重力ガスの熱平衡状態の安定性を検討した。基 本的な結論は、重力の寄与が大きくなると、熱平衡状態が不安定になるという ことであった。

このあとどうなるかということを調べるためには、数値計算をする必要 がある。 Hachisu et al. (1978) は、自己重力流体についてそのよう な数値計算を行なった。

結果の詳細は省くが、重要なことは、中心から熱をとったときに「自己相似解」 が現れる場合があるということである。

中心に熱を与えると、中心は温度を下げつつ膨張する。このときは、結局最終 的には安定平衡にいってしまうことになる。しかし、中心から熱をとったとき にはどこかいき先があるわけではない。

この後の進化は、熱伝導のタイムスケールによる。密度が上がるとタイムスケー ルが長くなるような場合には、大雑把にいってかなり大きなものが全体として 収縮していく。

これに対し、恒星系に対応する場合では、密度が上がるとタイムスケー ルが短くなる。この時は、密度の高い「コア」が出来、それがどんどん収縮を 続けるということになる。これに関する詳細な解析は Lynden-Bell & Eggleton (1980, MNRAS 191, 483) に与えられているので以下考え方だけを示 す。

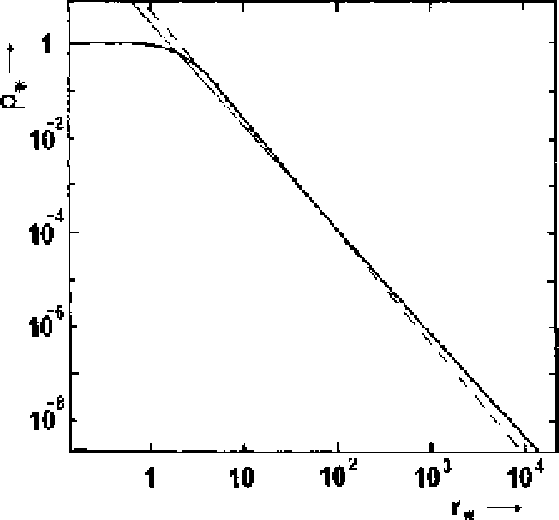
自己相似解というのは、ある物理量 $y$が

$$y(r,t) = y_0(t)y_*[r/r_0(t)].$$ (1)

と書けるようなものである。さらに、 $r_0$ と $y_0$ が時間のベキで書ける （これは数値計算の結果がそうなっている）とすれば、

$$r_0 = (t_0 - t)^{\beta},$$ (2)

とか

$$y_0 = (t_0 - t)^{\gamma},$$ (3)

と書け、結局

$$y_0 = r_0^{\gamma/\beta}.$$ (4)

という関係が出てくる。

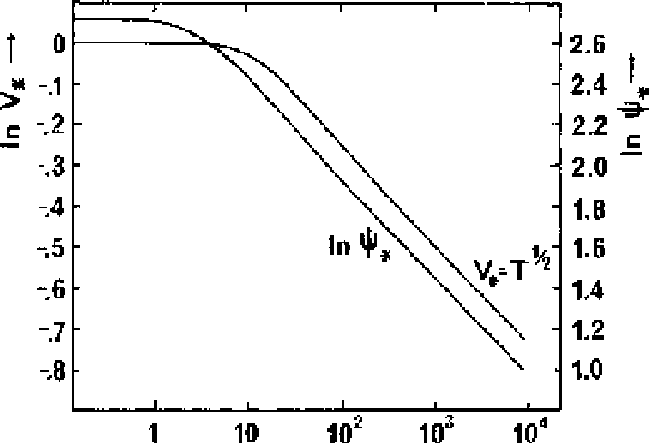
自己相似解ということで、いろんな無次元量は一定と考えられる。特に、今コ アというものを考えて、その半径を $r_c$ とすれば

$$\sigma^2 \propto\displaystyle{GM_c \over r_c} \sim {\rho_0 r_0^2}.$$ (5)

ここで $\rho_0$ を

$$\rho_0 = r_0^{\alpha},$$ (6)

と書けば

$$r_0 = (t_0 - t)^{2/(6+\alpha)}.$$ (7)

となる。

実際に $r_0(t)$ とかを求めるには、やはり固有値問題をとくことになる。 Lynden-Bell & Eggleton は実際にといて、

$$\rho = r^{-2.21}.$$ (8)

という答を得た。以下に、彼らの求めた固有関数を示す。

7cm 8cm

1.1 ガスと$N$体の違い

実は、このあたりの進化、すなわち重力熱力学的不安定や自己相似解について は、ガス近似、FP計算、$N$体の間の一致は素晴らしくよい。ガスではうまく 表現出来なくなるのは、質量分布がある場合、非等方性が発達する場合等であ る。